【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0),D(﹣7,3),点B、C在第二象限内.
(1)求点B的坐标。
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)B(﹣3,1);
(2)t的值为9,反比例函数解析式为y=![]() ;
;
(3)符合题意的点P、Q的坐标为P(![]() ,0)、Q(
,0)、Q(![]() ,4)或P(7,0)、Q(3,2).
,4)或P(7,0)、Q(3,2).
【解析】(1)过程略B(﹣3,1)
解:(2)设反比例函数为y=![]() ,
,
由题意得:点B′坐标为(﹣3+t,1),点D′坐标为(﹣7+t,3),
∵点B′和D′在该比例函数图象上,
∴k=(﹣3+t)×1=(﹣7+t)×3,[来源:]
解得:t=9,k=6,
∴反比例函数解析式为y=![]() .
.
(3) )假设存在,设点P的坐标为(m,0),点Q的坐标为(n,![]() ).
).
以P、Q、B′、D′四个点为顶点的四边形是平行四边形分两种情况:
①当B′D′为对角线时,设线段B′D′的中点为M,如图2所示.

∵点B′(6,1),点D′(2,3),点M为线段B′D′的中点,
∴点M的坐标为(4,2),
∵点M是线段PQ的中点,
∴ ,解得:
,解得:![]() ,
,
∴P(![]() ,0),Q(
,0),Q(![]() ,4);
,4);
②当B′D′为边时.
∵四边形PQB′D′为平行四边形,
∴ ,解得:
,解得:![]() ,
,
∴P(7,0),Q(3,2).
综上可知:存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形,符合题意的点P、Q的坐标为P(![]() ,0)、Q(
,0)、Q(![]() ,4)或P(7,0)、Q(3,2).
,4)或P(7,0)、Q(3,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的(探究).
(提出问题)两个有理数a、b满足a、b同号,求
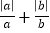 的值.
的值.(解决问题)解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则
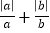 =
=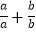 =1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则
=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则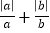 =
= =(﹣1)+(﹣1)=﹣2,所以
=(﹣1)+(﹣1)=﹣2,所以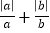 的值为2或﹣2.
的值为2或﹣2.(探究)请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求
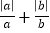 的值;
的值;(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y1=
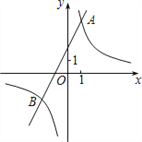
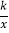 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2017将与圆周上的哪个数字重合( )
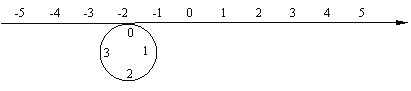
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
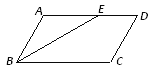
查看答案和解析>>【题目】平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为__________________cm.
-
科目: 来源: 题型:
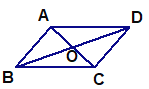
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,其中AC+BD=14,CD=5.
(1)若四边形ABCD是平行四边形,则△OCD的周长为_____________;
(2) 若四边形ABCD是矩形,则AD的长为_____________;
(3) 若四边形ABCD是菱形,则菱形的面积为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的集合内:
100,﹣0.82,﹣30
 ,3.14,﹣2,0,﹣2011,﹣3.1
,3.14,﹣2,0,﹣2011,﹣3.1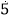 ,
, ,﹣
,﹣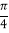 ,2.010010001…,
,2.010010001…,正分数集合:{ …}
整数集合:{ …}
负有理数集合:{ …}
非正整数集合;{ …}
无理数集合:{ …}.
相关试题

