【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

参考答案:
【答案】(1)BE是⊙O的切线;(2)![]() .
.
【解析】试题分析:(1)结论:BE是⊙O的切线.首先证明∠OAP=90°,再证明△EOB≌△EOA,推出∠OBE=∠OAE即可解决问题.
(2)由(1)可知AB=2BF,在Rt△BEO中,∠OBE=90°,OB=4,BE=3,可得OE=![]() =5,由
=5,由![]() BEOB=
BEOB=![]() OEBF,可得BF=
OEBF,可得BF=![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
试题解析:(1)BE是⊙O的切线.
理由:如图连接OA.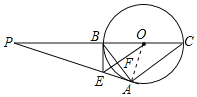
∵PA是切线,
∴PA⊥OA,
∴∠OAP=90°,
∵BC是直径,
∴∠BAC=90°,
∵OE∥AC,
∴∠OFB=∠BAC=90°,
∴OE⊥AB,
∴BF=FA,
∵OB=OA,
∴∠EOB=∠EOA,
在△EOB和△EOA中,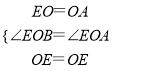 ,
,
∴△EOB≌△EOA,
∴∠OBE=∠OAE=90°,
∴OB⊥BE,
∴BE是⊙O的切线.
(2)由(1)可知AB=2BF,
在Rt△BEO中,∵∠OBE=90°,OB=8,BE=6,
∴OE=![]() =5,
=5,
∵![]() BEOB=
BEOB=![]() OEBF,
OEBF,
∴BF=![]() =
=![]() ,
,
∴AB=2BF=![]()
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
-
科目: 来源: 题型:
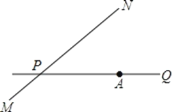
查看答案和解析>>【题目】如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD的边AB延长至点E,使BE=AB,连接DE、EC、BD、DE交BC于点O.
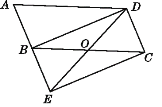
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=
 S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:已知:如图,
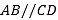 ,
,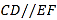 .求证:
.求证: .
.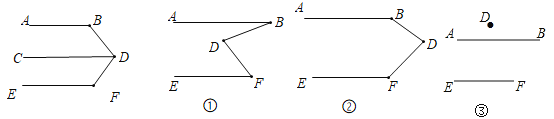
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变形,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线
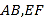 ,然后在平行线间画了一点
,然后在平行线间画了一点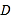 ,连接
,连接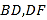 后,用鼠标拖动点
后,用鼠标拖动点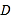 ,分别得到了图
,分别得到了图
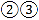 ,小颖发现图
,小颖发现图 正是上面题目的原型,于是她由上题的结论猜想到图
正是上面题目的原型,于是她由上题的结论猜想到图 和
和 图中的与
图中的与 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.请你在小颖操作探究的基础上,继续完成下面的问题:
(ⅰ)猜想图
 中
中 与
与 之间的数量关系并加以证明;
之间的数量关系并加以证明;(ⅱ)补全图
 ,直接写出
,直接写出 与
与 之间的数量关系: .
之间的数量关系: .
相关试题

