【题目】如图,将ABCD的边AB延长至点E,使BE=AB,连接DE、EC、BD、DE交BC于点O.
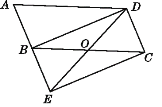
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)先运用平行四边形的知识得到AB=BE、BE=DC、BD=EC,即可证明△ABD≌△BEC;
(2)由四边形BECD为平行四边形可得OD=OE,OC=OB,再结合四边形ABCD为平行四边形得到∠A=∠OCD,再结合已知条件可得OC=OD,即BC=ED;最后根据对角线相等的平行四边形是矩形证明即可.
证明:(1)∵在平行四边形ABCD
∴AD=BC,AB=CD,AB∥CD,即BE∥CD.
又∵AB=BE,
∴BE=DC.
∴四边形BECD为平行四边形.
∴BD=EC.
在△ABD与△BEC中,
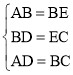
∴△ABD≌△BEC(SSS);
(2)∵四边形BECD为平行四边形,
∴ OD=OE,OC=OB,
∵四边形ABCD为平行四边形,
∴∠A=∠BCD.即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC
∴OC=OD.
∴OC+OB=OD+OE,即BC=ED.
∴四边形BECD为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的相伴方程.
(1)在方程
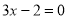 ①,
①, ②,
②, ③中,写出是不等式组
③中,写出是不等式组 的相伴方程的序号 .
的相伴方程的序号 .(2)写出不等式组
 的一个相伴方程,使得它的根是整数: .
的一个相伴方程,使得它的根是整数: .(3)若方程
 都是关于
都是关于 的不等式组
的不等式组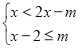 的相伴方程,求
的相伴方程,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?
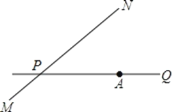
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=
 S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.
相关试题

