【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=_____,n=_____;
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x=_____.
时,x=_____.
②写出该函数的一条性质_____.
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是_____.
=t有两个不相等的实数根,则t的取值范围是_____.
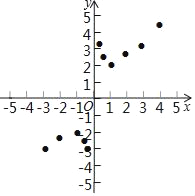
参考答案:
【答案】(1)x≠0;(2)![]() ;
;![]() ;(3)见解析;(4)①﹣4或﹣
;(3)见解析;(4)①﹣4或﹣![]() ;②函数图象在第一、三象限且关于原点对称;③t<﹣2或t>2.
;②函数图象在第一、三象限且关于原点对称;③t<﹣2或t>2.
【解析】
(1)由分母不为0,可得自变量x的取值范围:x≠0.
(2)根据图表可知,m,n分别为当![]() 和x=3时的函数值,代入解析式:
和x=3时的函数值,代入解析式:![]() 即可.
即可.
(3)根据描出的点连成平滑的曲线即可.
(4)①观察函数图像,结合(2)中的表格中,当![]() 时,x=4或
时,x=4或![]() 可得;当
可得;当![]() 时,x=-4或
时,x=-4或![]() .
.
②观察函数的图象写出函数的一条性质即可(增减性、对称性、图像所在象限等).
③此方程的根可看作![]() 和y=t的交点,故方程有两个不相等的实数根可看作是两个函数的图像有两个交点,观察图像可知,当t>2或t<-2时两函数的图像有两个交点,故t的取值范围为:t>2或t<-2.
和y=t的交点,故方程有两个不相等的实数根可看作是两个函数的图像有两个交点,观察图像可知,当t>2或t<-2时两函数的图像有两个交点,故t的取值范围为:t>2或t<-2.
解:(1)∵x在分母上,
∴x≠0.
故答案为:x≠0.
(2)当x=![]() 时,y=x+
时,y=x+![]() =
=![]() ;
;
当x=3时,y=x+![]() =
=![]() .
.
故答案为:![]() ;
;![]() .
.
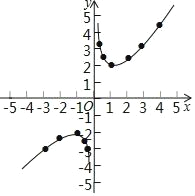
(3)连点成线,画出函数图象.
(4)①当y=﹣![]() 时,有x+
时,有x+![]() =﹣
=﹣![]() ,
,
解得:x1=﹣4,x2=﹣![]() .
.
故答案为:﹣4或﹣![]() .
.
②观察函数图象,可知:函数图象在第一、三象限且关于原点对称.
故答案为:函数图象在第一、三象限且关于原点对称.
③∵x+![]() =t有两个不相等的实数根,
=t有两个不相等的实数根,
∴t<﹣2或t>2.
故答案为:t<﹣2或t>2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,观察被开方数
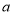 的小数点与算术平方根
的小数点与算术平方根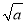 的小数点的移动规律:
的小数点的移动规律:
0.0016
0.16
16
1600
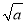
0.04
0.4
(2)根据你发现的规律填空:
①已知
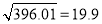 ,则
,则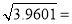 .
.②已知
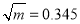 ,
,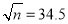 ,则
,则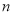 是
是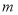 的 倍.
的 倍. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“奇巧数”,如
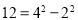 ,
, ,
,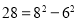 ,,因此
,,因此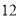 ,
,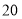 ,
,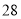 都是奇巧数.
都是奇巧数.(1)
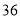 ,
,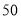 是奇巧数吗?为什么?
是奇巧数吗?为什么?(2)设两个连续偶数为
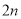 ,
,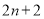 (其中
(其中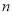 为正整数),由这两个连续偶数构造的奇巧数是4的倍数吗?为什么?
为正整数),由这两个连续偶数构造的奇巧数是4的倍数吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】材料:一般地,若
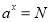 (
(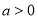 且
且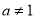 ),那么
),那么 叫做以
叫做以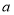 为底
为底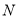 的对数,记作
的对数,记作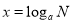 ,比如指数式
,比如指数式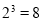 可以转化为对数式
可以转化为对数式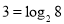 ,对数式
,对数式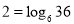 可以转化为指数式
可以转化为指数式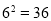 .
.根据以上材料,解决下列问题:
(1)计算:
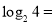 ,
,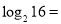 ,
,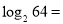 ;
;(2)观察(1)中的三个数,猜测:
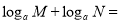 (
(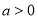 且
且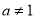 ,
,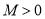 ,
, ),并加以证明这个结论;
),并加以证明这个结论;(3)已知:
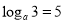 ,求
,求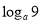 和
和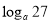 的值(
的值(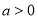 且
且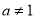 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,正方形ABCD是由两个长为a、宽为b的长方形和两个边长分别为a、b的正方形拼成的.
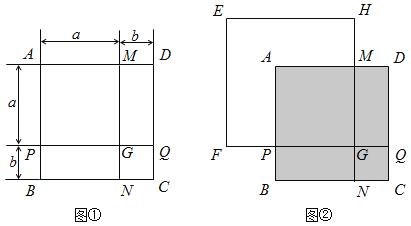
(1)利用正方形ABCD面积的不同表示方法,直接写出
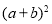 、
、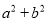 、ab之间的关系式,这个关系式是 ;
、ab之间的关系式,这个关系式是 ;(2)若m满足
 ,请利用(1)中的数量关系,求
,请利用(1)中的数量关系,求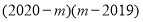 的值;
的值;(3)若将正方形EFGH的边
 、
、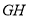 分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=
 (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
 在第一象限图象上一点,连接OA,过点A作AB∥x轴(点B在点A右侧),连接OB,若OB平分∠AOX,且点B的坐标是(8,4),则k的值是( )
在第一象限图象上一点,连接OA,过点A作AB∥x轴(点B在点A右侧),连接OB,若OB平分∠AOX,且点B的坐标是(8,4),则k的值是( )
A.6B.8C.12D.16
相关试题

