【题目】如图,已知抛物线![]() 的顶点C在x轴正半轴上,一次函数
的顶点C在x轴正半轴上,一次函数![]() 与抛物线交于A、B两点,与x、y轴交于D、E两点.
与抛物线交于A、B两点,与x、y轴交于D、E两点.

(1)求m的值.
(2)求A、B两点的坐标.
(3)点P(a,b)(![]() )是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
)是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
参考答案:
【答案】(1)3;(2)A(1,4),B(6,9);(3)![]() =
=![]() ,
,![]() =
=![]() .
.
【解析】
试题分析:(1)抛物线的顶点在x轴的正半轴上可知其对应的一元二次方程有两个相等的实数根,根据判别式等于0可求得m的值;
(2)由(1)可求得抛物线解析式,联立一次函数和抛物线解析式可求得A、B两点的坐标;
(3)分别过A、B、P三点作x轴的垂线,垂足分别为R、S、T,可先求得△ABC的面积,再利用a、b表示出△PAB的面积,根据面积之间的关系可得到a、b之间的关系,再结合P点在抛物线上,可得到关于a、b的两个方程,可求得a、b的值.
试题解析:(1)∵抛物线![]() 的顶点C在x轴正半轴上,∴方程
的顶点C在x轴正半轴上,∴方程![]() 有两个相等的实数根,∴
有两个相等的实数根,∴![]() ,解得m=3或m=﹣9,又抛物线对称轴大于0,即m+3>0,∴m=3;
,解得m=3或m=﹣9,又抛物线对称轴大于0,即m+3>0,∴m=3;
(2)由(1)可知抛物线解析式为![]() ,联立一次函数
,联立一次函数![]() ,可得
,可得 ,解得:
,解得:![]() 或
或![]() ,∴A(1,4),B(6,9);
,∴A(1,4),B(6,9);
(3)如图,分别过A、B、P三点作x轴的垂线,垂足分别为R、S、T,

∵A(1,4),B(6,9),C(3,0),P(a,b),∴AR=4,BS=9,RC=3﹣1=2,CS=6﹣3=3,RS=6﹣1=5,PT=b,RT=1﹣a,ST=6﹣a,∴S△ABC=S梯形ABSR﹣S△ARC﹣S△BCS=![]() ×(4+9)×5﹣
×(4+9)×5﹣![]() ×2×4﹣
×2×4﹣![]() ×3×9=15,S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP=
×3×9=15,S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP=![]() (9+b)(6﹣a)﹣
(9+b)(6﹣a)﹣![]() (b+4)(1﹣a)﹣
(b+4)(1﹣a)﹣![]() ×(4+9)×5=
×(4+9)×5=![]() (5b-5a﹣15),又S△PAB=2S△ABC,∴
(5b-5a﹣15),又S△PAB=2S△ABC,∴![]() (5b-5a﹣15)=30,即b-a=15,∴b=15+a,∵P点在抛物线上,∴
(5b-5a﹣15)=30,即b-a=15,∴b=15+a,∵P点在抛物线上,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∵
,∵![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,

(1)请用含t的代数式分别表示出点C与点P的坐标;
(2)以点C为中心,
 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.①当⊙C与射线DE有公共点时,求t的取值范围;
②当△PAB为等腰三角形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于点F,交AC于点E,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+
 ∠C;②AE+BF=EF;③当∠C=90°时,E、F分别是AC、BC的中点;④若OD=
∠C;②AE+BF=EF;③当∠C=90°时,E、F分别是AC、BC的中点;④若OD= CE+CF=
CE+CF= 则S△CEF=
则S△CEF=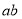 ,其中正确的是______________
,其中正确的是______________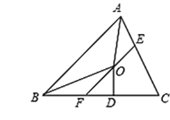
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若
 =2,求
=2,求 的值;
的值;(3)若
 =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?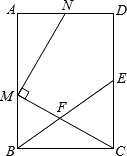
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》卷九“勾股”中记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问霞长几何.
注释:今有正方形水池边长1丈,芦苇生长在中央,长出水面1尺.将芦苇向池岸牵引,恰好与水岸齐,问芦苇的长度(一丈等于10尺).解决下列问题:
(1)示意图中,线段
 的长为______尺,线段
的长为______尺,线段 的长为______尺;
的长为______尺;
(2)求芦苇的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①
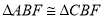 ;②点E到AB的距离是
;②点E到AB的距离是 ;③
;③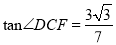 ;④△ABF的面积为
;④△ABF的面积为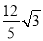 .其中一定成立的有几个( )
.其中一定成立的有几个( )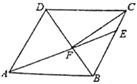
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

