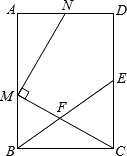
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() =2,求
=2,求![]() 的值;
的值;
(3)若![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
参考答案:
【答案】(1)详见解析;(2)3;(3)n=4.
【解析】
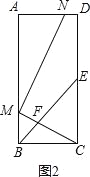
试题分析:(1)如图1,易证△BMF≌△ECF,则有BM=EC,然后根据E为CD的中点及AB=DC就可得到AM=EC;(2)如图2,设MB=a,易证△ECF∽△BMF,根据相似三角形的性质可得EC=2a,由此可得AB=4a,AM=3a,BC=AD=2a.易证△AMN∽△BCM,根据相似三角形的性质即可得到AN=![]() a,从而可得ND=AD﹣AN=
a,从而可得ND=AD﹣AN=![]() a,就可求出
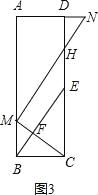
a,就可求出![]() 的值;(3)如图3,设MB=a,同(2)可得BC=2a,CE=na.由MN∥BE,MN⊥MC可得∠EFC=∠HMC=90°,从而可证到△MBC∽△BCE,然后根据相似三角形的性质即可求出n的值.
的值;(3)如图3,设MB=a,同(2)可得BC=2a,CE=na.由MN∥BE,MN⊥MC可得∠EFC=∠HMC=90°,从而可证到△MBC∽△BCE,然后根据相似三角形的性质即可求出n的值.
试题解析:(1)当F为BE中点时,如图1,
则有BF=EF.
∵四边形ABCD是矩形,
∴AB=DC,AB∥DC,
∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,
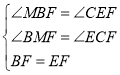 ,
,
∴△BMF≌△ECF,
∴BM=EC.
∵E为CD的中点,
∴EC=![]() DC,
DC,
∴BM=EC=![]() DC=
DC=![]() AB,
AB,
∴AM=BM=EC;
(2)如图2,
设MB=a,
∵四边形ABCD是矩形,
∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,
∴△ECF∽△BMF,
∴![]() =2,
=2,
∴EC=2a,
∴AB=CD=2CE=4a,AM=AB﹣MB=3a.
∵![]() =2,
=2,
∴BC=AD=2a.
∵MN⊥MC,
∴∠CMN=90°,
∴∠AMN+∠BMC=90°.
∵∠A=90°,
∴∠ANM+∠AMN=90°,
∴∠BMC=∠ANM,
∴△AMN∽△BCM,
∴![]() ,
,
∴![]() ,
,
∴AN=![]() a,ND=AD﹣AN=2a﹣
a,ND=AD﹣AN=2a﹣![]() a=
a=![]() a,
a,
∴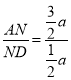 =3;
=3;
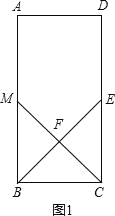
(3)当![]() =n时,如图3,
=n时,如图3,
设MB=a,同(2)可得BC=2a,CE=na.
∵MN∥BE,MN⊥MC,
∴∠EFC=∠HMC=90°,
∴∠FCB+∠FBC=90°.
∵∠MBC=90°,
∴∠BMC+∠FCB=90°,
∴∠BMC=∠FBC.
∵∠MBC=∠BCE=90°,
∴△MBC∽△BCE,
∴![]() ,
,
∴![]() ,
,
∴n=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
93
89
90
学生乙
94
92
94
86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据2,7,5,7,9的众数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:4y﹒(-2xy2)=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)a5﹣a3
(2)4﹣4(x﹣y)+(x﹣y)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】试写出一个关于x的二次三项式,使二次项系数为2,一次项系数为3,常数项为-5,答案是_.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区教育局对本区教师个人的每学期绩效工资进行抽样问卷调查,并将调查结果整理后制作了如下不完整的统计图表:
某区教师个人绩效工资统计表
分组
个人学期绩效工资x(元)
频数(人)
频率
A
x≤2000
18
0.15
B
2000<x≤4000
a
b
C
4000<x≤6000
D
6000<x≤8000
24
0.20
E
x>8000
12
0.10
合计
c
1.00
根据以上图表中信息回答下列问题:
(1)直接写出结果a= ;b= ;c= ;并将统计图表补充完整;
(2)教师个人的每学期绩效工资的中位数出现在第 组;
(3)已知该区共有教师5000人,请你估计教师个人每学期绩效工资在6000元以上(不含6000元)的人数.

相关试题

