【题目】已知:如图,一次函数y=kx﹣1的图象经过点A(3![]() ,m)(m>0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.
,m)(m>0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.
(1)求这个一次函数的表达式;
(2)已知一开口向下、以直线CD为对称轴的抛物线经过点A,它的顶点为P,若过点P且垂直于AP的直线与x轴的交点为Q(﹣![]() ,0),求这条抛物线的函数表达式.
,0),求这条抛物线的函数表达式.

参考答案:
【答案】(1)y=![]() x﹣1;(2)抛物线解析式为:y=
x﹣1;(2)抛物线解析式为:y=![]()
【解析】(1)利用三角形相似和勾股定理构造方程,求AC和m
(2)由∠APQ=90°,构造△PQD∽△APE构造方程求点P坐标可求二次函数解析式.
(1)过点A作AF⊥x轴,过点B作BF⊥CD于H,交AF于点F,过点C作CE⊥AF于点E.
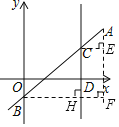
设AC=n,则CD=n
∵点B坐标为(0,-1)
∴CH=n+1,AF=m+1
∵CH∥AF,BC=2AC
∴![]() ,即:
,即:![]()
整理得:
n=![]()
Rt△AEC中,
CE2+AE2=AC2
∴5+(m-n)2=n2
把n=![]() 代入,得:
代入,得:![]()
解得m1=5,m2=-3(舍去)
∴n=3
∴把A(3![]() ,5)代入y=kx-1得
,5)代入y=kx-1得
k=![]()
∴y=![]() x-1
x-1
(2)如图,过点A作AE⊥CD于点E
设点P坐标为(2![]() ,n),由已知n>0
,n),由已知n>0
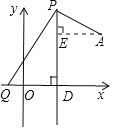
由已知,PD⊥x轴,易证△PQD∽△APE,
∴![]() ,
,
∴![]() ,
,
解得n1=7,n2=-2(舍去).
设抛物线解析式为y=a(x-h)2+k
∴y=a(x-2![]() )2+5
)2+5
把A(3![]() ,5)代入y=a(x-2
,5)代入y=a(x-2![]() )2+7
)2+7
解得a=-![]()
∴抛物线解析式为:y=-![]() x2+
x2+![]() x1
x1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB=17,CD=10,∠A=90°,cosB=
 ,求AD的长.
,求AD的长.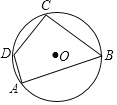
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点B的坐标为(6,4).
(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.
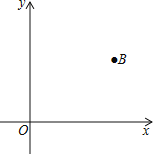
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若
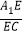 =
= ﹣1,求
﹣1,求 的值.
的值.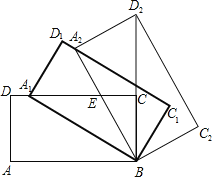
-
科目: 来源: 题型:
查看答案和解析>>【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
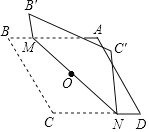
A. 7 B. 6 C. 5 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个变量x,y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出y的变化范围;
(2)求当x=0,-3时,y的对应值;
(3)求当y=0,3时,对应的x的值;
(4)当x为何值时,y的值最大?
(5)当x在什么范围内时,y的值在不断增加?
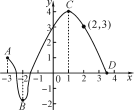
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
相关试题

