【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α度时,判定四边形A1BCE的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)四边形A1BCE是菱形.
【解析】
试题分析:(1)根据等腰三角形的性质得到AB=BC,∠A=∠C,由旋转的性质得到A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,根据全等三角形的判定定理得到△BCF≌△BA1D;
(2)由旋转的性质得到∠A1=∠A,根据平角的定义得到∠DEC=180°﹣α,根据四边形的内角和得到∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α,证得四边形A1BCE是平行四边形,由于A1B=BC,即可得到四边形A1BCE是菱形.
试题解析:(1)证明:∵△ABC是等腰三角形,∴AB=BC,∠A=∠C,∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,∴A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,在△BCF与△BA1D中,∵∠A1=∠C,A1B=BC,∠A1BD=∠CBF,∴△BCF≌△BA1D;
(2)解:四边形A1BCE是菱形,∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,∴∠A1=∠A,∵∠ADE=∠A1DB,∴∠AED=∠A1BD=α,∴∠DEC=180°﹣α,∵∠C=α,∴∠A1=α,∴∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α,∴∠A1=∠C,∠A1BC=∠AEC,∴四边形A1BCE是平行四边形,∴A1B=BC,∴四边形A1BCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6.将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.
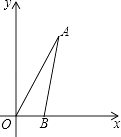
(1)请在图中画出△COD;
(2)求点A旋转过程中所经过的路程(精确到0.1). -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2+2a+1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组式的变形过程,然后回答问题: 例1:
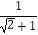 =
= 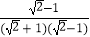 =
= 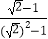 =
= 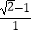 =
= 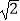 ﹣1.
﹣1.
例2: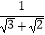 =
= 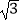 ﹣
﹣ 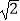 ,
, 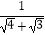 =
= 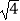 ﹣
﹣ 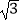 ,
, 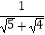 =
= 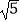 ﹣
﹣ 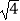
利用以上结论解答以下问题:
(1)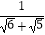 =;
=; 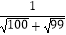 =;
=;
(2)你用含n(n为正整数)的关系式表示上述各式子的变形规律.
(3)应用上面的结论,求下列式子的值.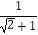 +
+ 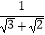 +
+ 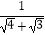 +…+
+…+ 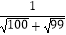
(4)拓展提高,求下列式子的值.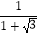 +
+ 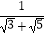 +
+ 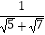 +…+
+…+ 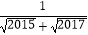 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE=
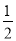 (AB+AC).
(AB+AC).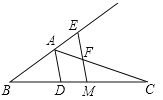
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置,那么.
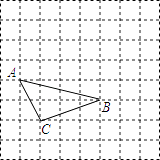
(1)画出直角坐标系;
(2)画出与△ABC关于x轴对称的图形△DEF;
(3)P为x轴上的一个动点,是否存在P使PA+PB的值最小?若不存在,请说明理由;若存在请求出点P的坐标和PA+PB的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一海轮位于灯塔P的西南方向,距离灯塔40了2海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).

相关试题

