【题目】如图,一海轮位于灯塔P的西南方向,距离灯塔40了2海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).

参考答案:
【答案】![]() 海里
海里
【解析】试题分析:过P作PC垂直于AB,在直角三角形ACP中,利用锐角三角函数定义求出AC与PC的长,在直角三角形BCP中,利用锐角三角函数定义求出CB的长,由AC+CB求出AB的长即可.
试题解析:
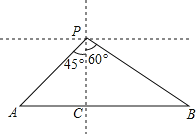
过P作PC⊥AB于点C,
在Rt△ACP中,PA=![]() 海里,∠APC=45°,sin∠APC=
海里,∠APC=45°,sin∠APC=![]() ,cos∠APC=
,cos∠APC=![]() ,
,
∴AC=APsin45°=![]() ×
×![]() =40(海里),PC=APcos45°=
=40(海里),PC=APcos45°=![]() ×
×![]() =40(海里),
=40(海里),
在Rt△BCP中,∠BPC=60°,tan∠BPC=![]() ,
,
∴BC=PCtan60°=![]() (海里),
(海里),
则AB=AC+BC=(40+![]() )海里。
)海里。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α度时,判定四边形A1BCE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE=
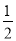 (AB+AC).
(AB+AC).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置,那么.
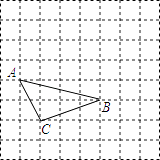
(1)画出直角坐标系;
(2)画出与△ABC关于x轴对称的图形△DEF;
(3)P为x轴上的一个动点,是否存在P使PA+PB的值最小?若不存在,请说明理由;若存在请求出点P的坐标和PA+PB的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为
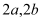 ,点A、D、G在
,点A、D、G在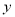 轴上,坐标原点O为AD的中点,抛物线
轴上,坐标原点O为AD的中点,抛物线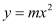 过C、F两点,连接FD并延长交抛物线于点M.
过C、F两点,连接FD并延长交抛物线于点M.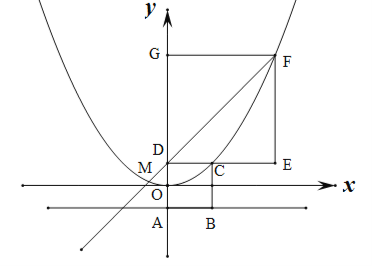
(1)若
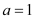 ,求m和b的值;
,求m和b的值;(2)求
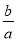 的值;
的值;(3)判断以FM为直径的圆与AB所在直线的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.

(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面上四个点A,B,C,D. 按要求完成下列问题:
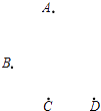
(1)①连接AC,BD;②画射线AB与直线CD相交于点E;
(2)用量角器度量∠AED的大小为(精确到度).
相关试题

