Question

【题目】如图，将正n边形绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为“叠弦角”，△AOP为“叠弦三角形”．

【探究证明】

⑴请在图1和图2中选择其中一个证明：“叠弦三角形”(△AOP)是等边三角形；

⑵如图2，求证：∠OAB=∠OAE′．

图1(n=4) 图2(n=5) 图3(n=6) 图n

【归纳猜想】

⑶图1、图2中的“叠弦角”的度数分别为_____________，_________；

⑷图n中，“叠弦三角形”_____________等边三角形(填“是”或“不是”)

⑸图n中，“叠弦角”的度数为______________________(用含n的式子表示)

Answer 1

【答案】 15°， 24° 是 ．

【解析】（1）先由旋转的性质，再判断出△APD≌△AOD/，最后用旋转角计算即可；

（2）向判断出Rt△AEM≌△Rt△ABN，在判断出Rt△APM≌Rt△AON即可；

（3）先判断出△AD/O≌△ABO，再利用正方形，正五边形的性质和旋转的性质，计算即可；

（4）先判断出△APF≌△AE/F/，再用旋转角60°，从而得出△PAO是等边三角形；

（5）用（3）的方法求出正n边形的“叠弦角”的度数.

解：（1）如图1，

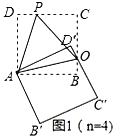
∵四边形ABCD是正方形， 由旋转知：AD=AD'，∠D=∠D'=90°，∠DAD'=∠OAP=60°，

∴∠DAP=∠D'AO，∴△APD≌△AOD'（ASA）∴AP=AO，

∵∠OAP=60°，∴△AOP是等边三角形，

（2）如图2，作AM⊥DE于M，作AN⊥CB于N．

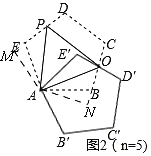
∵五边形ABCDE是正五边形，

由旋转知：AE=AE'，∠E=∠E'=108°，∠EAE'=∠OAP=60°

∴∠EAP=∠E'AO ∴△APE≌△AOE'（ASA）

∴∠OAE'=∠PAE．

在Rt△AEM和Rt△ABN中，∠AEM=∠ABN=72°，AE=AB

∴Rt△AEM≌Rt△ABN （AAS）， ∴∠EAM=∠BAN，AM=AN．

在Rt△APM和Rt△AON中，AP=AO，AM=AN

∴Rt△APM≌Rt△AON （HL）．∴∠PAM=∠OAN，

∴∠PAE=∠OAB ∴∠OAE'=∠OAB （等量代换）．

（3）由（1）有，△APD≌△AOD'，

∴∠DAP=∠D′AO，

在△AD′O和△ABO中，

AD′=AB，AO=AO，

∴△AD′O≌△ABO，∴∠D′AO=∠BAO，

由旋转得，∠DAD′=60°，∵∠DAB=90°，∴∠D′AB=∠DAB﹣∠DAD′=30°，

∴∠D′AD=∠D′AB=15°，

同理可得，∠E′AO=24°，

故答案为：15°，24°．

（4）如图3，

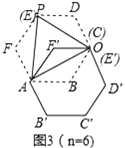
∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形，∴∠F=F′=120°，由旋转得，AF=AF′，EF=E′F′，∴△APF≌△AE′F′，∴∠PAF=∠E′AF′，

由旋转得，∠FAF′=60°，AP=AO ∴∠PAO=∠FAO=60°，

∴△PAO是等边三角形．故答案为：是

（5）图n中的多边形是正（n+3）边形，

同（3）的方法得，

故答案： ．