【题目】阅读下列材料,解决问题
材料一:如果一个正整数的个位数字等于除个位数字之外的其他各位数字之和,则称这个数为“刀塔数”,比如:因1+2=3,所以123是“刀塔数”,同理,55,1315也是“刀塔数”.
材料二:形如![]() 的三位数叫“王者数”,其中x﹣2,x,x+2分别是这个数的百位数字,十位数字,个位数字.例如:135,468均为“王者数”
的三位数叫“王者数”,其中x﹣2,x,x+2分别是这个数的百位数字,十位数字,个位数字.例如:135,468均为“王者数”
问题:
(1)已知a既是“刀塔数”又是“王者数”,若数b(b>0)使10a+b为一个“刀塔数”,求b的最小值;
(2)已知一个五位“刀塔数”![]() 与一个“王者数”的和能被3整除,且c﹣a+d﹣b=4,证明
与一个“王者数”的和能被3整除,且c﹣a+d﹣b=4,证明![]() .
.
参考答案:
【答案】(1)b的最小值为47;(2)见解析
【解析】试题分析:(1)仔细阅读材料,利用“王者数”和“刀塔数”的特点列方程求解即可求出b的最小值;
(2)根据“王者数”和“刀塔数”的特点,表示出a、b、c、d、e的关系,然后根据题意证明即可.
试题解析:(1)∵a是“王者数”,
∴设a=![]() ,
,
∵a是“刀塔数”,
∴x﹣2+x=x+2,
∴x=4,
∴a=246,
∴10a+b=2460+b,
∵2+4+6=10>9,
而10a+b是“刀塔数”,
∴b>40,
即:2460+b的百位最小是5,
∴b的最小值为47;
(2)∵五位“刀塔数”![]() ,
,
∴e=a+b+c+d,
∵c﹣a+d﹣b=4,
∴c+d=a+b+4,
∴e=2a+2b+4,
∵a,b,e是五位数的位上的数,
∴0<a≤9,0<b≤9,0<e≤9的整数,
∴0<2a+2b+4≤9,
∴0<a+b≤![]() ,
,
∴a+b=1或a+b=2,
∵一个五位“刀塔数”![]() 与一个“王者数”的和能被3整除,而一个“王者数”是3的倍数,
与一个“王者数”的和能被3整除,而一个“王者数”是3的倍数,
∴a+b+c+d+e=a+b+a+b+4+2a+2b+4=4a+4b+8=4(a+b+2)是3的倍数,
即:a+b+2是3的倍数,
∴a+b=1,
∵a是最高位数字,
∴a=1,b=0,
∴c+d=a+b+4=5,e=2a+2b+4=6,而c在百位,d在十位,
∴c=5,d=0时,五位数大,
∴五位“刀塔数”![]() 最大是10506,
最大是10506,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市正在开展“食品安金城市”创建活动,为了调查学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷.将调查结果按照“
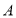 :正常了解;
:正常了解;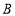 :了解;
:了解;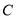 :了解较少;
:了解较少;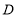 :不了解”四类分别进行统计,并绘制了如图所示的两幅统计图(不完整).
:不了解”四类分别进行统计,并绘制了如图所示的两幅统计图(不完整).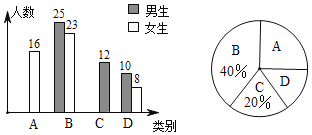
请根据图中信息,解答下列问题:
(1)此次共调查了_____名学生;
(2)扇形统计图中
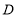 所在扇形的圆心角度数为_____度;
所在扇形的圆心角度数为_____度;(3)将条形统计图补充完整;
(4)若该校共有
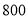 名学生,请你估计对食品安全知识“非常了解”的学生人数.
名学生,请你估计对食品安全知识“非常了解”的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求
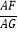 的值.
的值.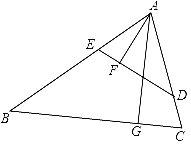
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m,n,p满足m<n<p(mp<0)且|p|<|n|<|m|,则|x﹣m|+|x+n|+|x+p|的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强
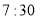 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留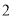 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚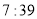 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早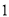 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程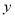 (千米)与行驶时间
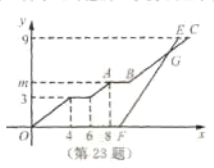
(千米)与行驶时间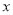 (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.(1)求点
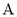 的纵坐标
的纵坐标 的值;
的值;(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
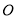 是直线
是直线 上一点,
上一点, 为任一条射线,
为任一条射线, 平分
平分 ,
, 平分
平分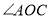 .
.
(1)找出图中
 的补角,
的补角,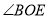 的补角;
的补角;(2)若
 ,求
,求 和
和 的度数;
的度数;(3)
 与
与 具有怎样的数量关系?说明理由.
具有怎样的数量关系?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个菱形的两个顶点与一个正方形的两个顶点重合,并且这两个四边形没有公共边,菱形的面积为24cm2,正方形的面积为32cm2,则菱形的边长为______________cm.
相关试题

