【题目】如图,![]() 是直线
是直线![]() 上一点,
上一点,![]() 为任一条射线,
为任一条射线,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.

(1)找出图中![]() 的补角,
的补角,![]() 的补角;
的补角;
(2)若![]() ,求
,求![]() 和
和![]() 的度数;
的度数;
(3)![]() 与
与![]() 具有怎样的数量关系?说明理由.
具有怎样的数量关系?说明理由.
参考答案:
【答案】(1)![]() 的补角
的补角![]() 或
或![]() ;
;![]() 的补角
的补角![]() 或
或![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)根据互为补角的和等于180°找出即可;
(2)根据角平分线的定义求出∠COD的度数即可,先求出∠AOC的度数,再根据角平分线的定义解答;
(3)根据角平分线的定义表示出∠COD与∠EOC,然后整理即可得解.
(1)∵OD平分∠BOC,
∴∠COD=∠BOD.
∵∠AOD+∠BOD=180°,
∴∠AOD的补角为∠BOD,∠COD.
同理:∠BOE的补角为∠AOE,∠COE;
(2)∵OD平分∠BOC,∠BOC=68°,
∴∠COD![]() ∠BOC
∠BOC![]() 68°=34°.
68°=34°.
∵∠BOC=68°,
∴∠AOC=180°﹣∠BOC=180°﹣68°=112°.
∵OE平分∠AOC,
∴∠EOC![]() ∠AOC
∠AOC![]() 112°=56°;
112°=56°;
(3)∵OD平分∠BOC,OE平分∠AOC,
∴∠COD![]() ∠BOC,∠EOC
∠BOC,∠EOC![]() ∠AOC,
∠AOC,
∴∠COD+∠EOC![]() (∠BOC+∠AOC)
(∠BOC+∠AOC)![]() 180°=90°,
180°=90°,
即∠COD+∠EOC=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m,n,p满足m<n<p(mp<0)且|p|<|n|<|m|,则|x﹣m|+|x+n|+|x+p|的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,解决问题
材料一:如果一个正整数的个位数字等于除个位数字之外的其他各位数字之和,则称这个数为“刀塔数”,比如:因1+2=3,所以123是“刀塔数”,同理,55,1315也是“刀塔数”.
材料二:形如
 的三位数叫“王者数”,其中x﹣2,x,x+2分别是这个数的百位数字,十位数字,个位数字.例如:135,468均为“王者数”
的三位数叫“王者数”,其中x﹣2,x,x+2分别是这个数的百位数字,十位数字,个位数字.例如:135,468均为“王者数”问题:
(1)已知a既是“刀塔数”又是“王者数”,若数b(b>0)使10a+b为一个“刀塔数”,求b的最小值;
(2)已知一个五位“刀塔数”
 与一个“王者数”的和能被3整除,且c﹣a+d﹣b=4,证明
与一个“王者数”的和能被3整除,且c﹣a+d﹣b=4,证明 .
. -
科目: 来源: 题型:
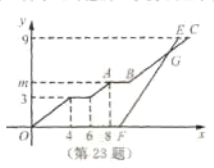
查看答案和解析>>【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强
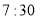 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留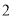 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚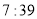 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早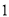 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程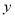 (千米)与行驶时间
(千米)与行驶时间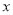 (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.(1)求点
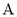 的纵坐标
的纵坐标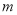 的值;
的值;(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个菱形的两个顶点与一个正方形的两个顶点重合,并且这两个四边形没有公共边,菱形的面积为24cm2,正方形的面积为32cm2,则菱形的边长为______________cm.
-
科目: 来源: 题型:
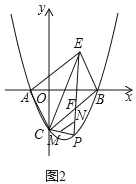
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线
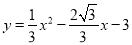 与x轴交于A、B两点(点A在点B左侧),与y轴交于C点,点E在第一象限且四边形ACBE为矩形.
与x轴交于A、B两点(点A在点B左侧),与y轴交于C点,点E在第一象限且四边形ACBE为矩形.(1)求∠BCE的度数;
(2)如图2,F为线段BC上一动点,P为第四象限内抛物线上一点,连接CP、FP、BP、EF,M,N分别是线段CP,FP的中点,连接MN,当△BCP面积最大,且MN+EF最小时,求PF的长度;
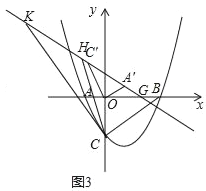
(3)如图3,将△AOC绕点O顺时针旋转一个角度α(0°<α<180°),点A,C的对应点分别为A',C',直线A'C'与x轴交于点G,G在x轴正半轴上且OG=
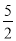 .线段KH在直线A'C'上平移( K在H左边),且KH=5,△KHC是否能成为等腰三角形?若能,请求出所有符合条件的点K的坐标;若不能,请说明理由.
.线段KH在直线A'C'上平移( K在H左边),且KH=5,△KHC是否能成为等腰三角形?若能,请求出所有符合条件的点K的坐标;若不能,请说明理由.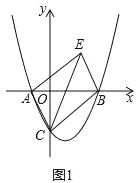
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“快乐分式”.如:
 ,则
,则  是“快乐分式”.
是“快乐分式”.(1)下列式子中,属于“快乐分式”的是 (填序号);
①
 ,②
,②  ,③
,③ ,④
,④  .
. (2)将“快乐分式”
 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为: = .
= . (3)应用:先化简
 ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
相关试题

