【题目】如图,在![]() 中,
中,![]() ,且
,且![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() ,
,![]() .①
.①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .则下列结论正确的是________.
.则下列结论正确的是________.
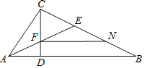
参考答案:
【答案】①②③④
【解析】
根据已知条件可证△ADC∽△CDB,得出∠ACB=90°.根据等量关系及等腰三角形的性质得到CF=BN.根据同位角相等,证明FN∥AB.证明△ADF∽△CDA,根据相似三角形的性质得出AD2=DFDC.
②∵CD⊥AB,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴△ADC∽△CDB,
∴∠ACD=∠B,
∴![]() ,故本选项正确;
,故本选项正确;
①∵AE平分∠CAB
∴∠CAE=∠DAF,
![]()
∴△CAE∽△DAF,
∴∠AFD=∠AEC,
∴∠CFE=∠AEC,
∴CF=CE,
∵CN=BE,
∴CE=BN,
∴CF=BN,故本选项正确;

③∵∠EAB=∠B,
∴EA=EB,
∵∠ACD=∠B,∠CAE=∠EAB,
∴∠ACD=∠CAE,
∴FA=FC,
∴FA=FC=BN,
EF=EN,
![]()
∠FEN=∠AEB,
∴△EFN∽△EAB,
∴∠EFN=∠EAB,
∴FN∥AB,故本选项正确;
④易证△ADF∽△CDA,
∴![]() 故本选项正确;
故本选项正确;
故答案为:①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形
 是正方形,
是正方形, 是
是 延长线上一点,直角三角尺的一条直角边经过点
延长线上一点,直角三角尺的一条直角边经过点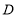 ,且直角顶点
,且直角顶点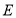 在
在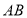 边上滑动(点
边上滑动(点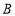 不与点
不与点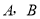 重合),另一条直角边与
重合),另一条直角边与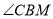 的平分线
的平分线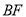 相交于点
相交于点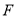 .
.(1)如图1所示,当点
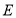 在
在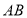 边的中点时:
边的中点时:①通过测量
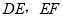 的长度,猜想
的长度,猜想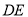 与
与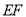 满足的数量关系是________________;
满足的数量关系是________________;②连接点
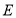 与
与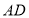 边的中点
边的中点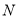 ,猜想
,猜想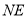 与
与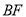 满足的数量关系是________________;
满足的数量关系是________________;③请证明上述你的两个猜想.
(2)如图2所示,当点
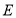 在
在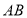 边上的任意位置时,请你在
边上的任意位置时,请你在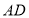 边上找到一点
边上找到一点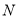 ,使得
,使得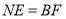 ,进而猜想此时
,进而猜想此时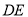 与
与 的数量关系.
的数量关系.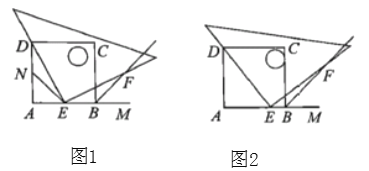
-
科目: 来源: 题型:
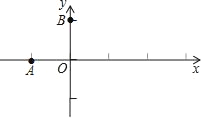
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 四个小球分别从正方形的四个顶点
四个小球分别从正方形的四个顶点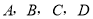 处出发(小球的大小忽略不计),以同样的速度分别沿
处出发(小球的大小忽略不计),以同样的速度分别沿 方向滚动,其终点分别是点
方向滚动,其终点分别是点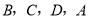 ,顺次连接四个小球所在的位置,得到四边形
,顺次连接四个小球所在的位置,得到四边形 .
.(1)不论小球滚动多长时间,求证;四边形
 总是正方形;
总是正方形;(2)这个四边形在什么时候面积最大?
(3)在什么时侯四边形
 的面积为正方形
的面积为正方形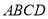 面积的一半?请说明理由.
面积的一半?请说明理由.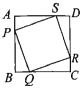
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
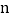 个边长为
个边长为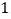 的相邻正方形的一边均在同一直线上,点
的相邻正方形的一边均在同一直线上,点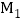 ,
,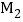 ,
,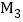 ,…
,…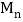 分别为边
分别为边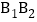 ,
,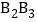 ,
,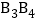 ,…,
,…,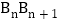 的中点,
的中点,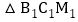 的面积为
的面积为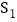 ,
,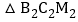 的面积为
的面积为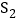 ,…
,…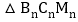 的面积为
的面积为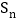 ,则
,则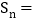 ________.(用含
________.(用含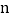 的式子表示)
的式子表示)
-
科目: 来源: 题型:
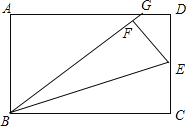
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若
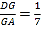 ,则
,则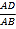 =__.
=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
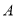 的坐标为
的坐标为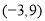 ,过点
,过点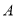 作
作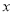 轴的垂线交
轴的垂线交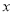 轴于点
轴于点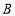 ,连接
,连接 ,现将
,现将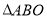 沿
沿 折叠,点
折叠,点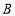 落在第一象限的
落在第一象限的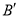 处,则直线
处,则直线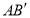 与
与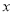 轴的交点
轴的交点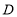 的坐标为( )
的坐标为( )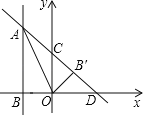
A.
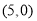 B.
B.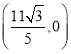 C.
C.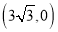 D.
D.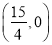
相关试题

