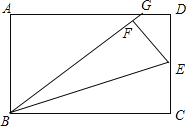
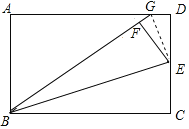
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
参考答案:
【答案】![]()
【解析】
连接GE,根据中点定义可得DE=CE,再根据翻折的性质可得DE=EF,∠BFE=90°,利用“HL”证明Rt△EDG≌Rt△EFG,根据全等三角形对应边相等可得FG=DG,根据![]() ,设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,由勾股定理求得AB=
,设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,由勾股定理求得AB=![]() ,再求比值即可.
,再求比值即可.
连接GE,
∵点E是CD的中点,∴EC=DE,
∵将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,
∴EF=DE,∠BFE=90°,
在Rt△EDG和Rt△EFG中![]() ,
,
∴Rt△EDG≌Rt△EFG(HL),
∴FG=DG,
∵![]() ,
,
∴设DG=FG=a,则AG=7a,故AD=BC=8a,则BG=BF+FG=9a,
∴AB=![]() ,
,
故![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 四个小球分别从正方形的四个顶点
四个小球分别从正方形的四个顶点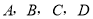 处出发(小球的大小忽略不计),以同样的速度分别沿
处出发(小球的大小忽略不计),以同样的速度分别沿 方向滚动,其终点分别是点
方向滚动,其终点分别是点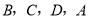 ,顺次连接四个小球所在的位置,得到四边形
,顺次连接四个小球所在的位置,得到四边形 .
.(1)不论小球滚动多长时间,求证;四边形
 总是正方形;
总是正方形;(2)这个四边形在什么时候面积最大?
(3)在什么时侯四边形
 的面积为正方形
的面积为正方形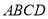 面积的一半?请说明理由.
面积的一半?请说明理由.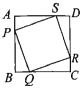
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
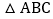 中,
中,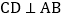 ,且
,且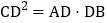 ,
,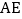 平分
平分 交
交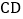 于
于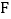 ,
,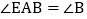 ,
,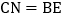 .①
.①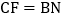 ;②
;②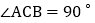 ;③
;③ ;④
;④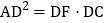 .则下列结论正确的是________.
.则下列结论正确的是________.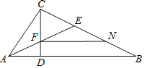
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
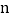 个边长为
个边长为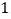 的相邻正方形的一边均在同一直线上,点
的相邻正方形的一边均在同一直线上,点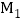 ,
,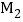 ,
,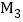 ,…
,…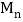 分别为边
分别为边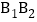 ,
,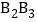 ,
,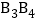 ,…,
,…,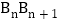 的中点,
的中点,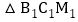 的面积为
的面积为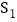 ,
,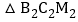 的面积为
的面积为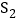 ,…
,…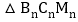 的面积为
的面积为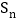 ,则
,则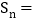 ________.(用含
________.(用含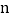 的式子表示)
的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
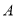 的坐标为
的坐标为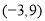 ,过点
,过点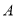 作
作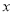 轴的垂线交
轴的垂线交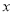 轴于点
轴于点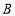 ,连接
,连接 ,现将
,现将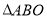 沿
沿 折叠,点
折叠,点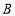 落在第一象限的
落在第一象限的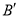 处,则直线
处,则直线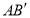 与
与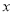 轴的交点
轴的交点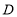 的坐标为( )
的坐标为( )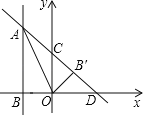
A.
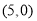 B.
B.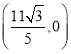 C.
C.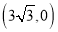 D.
D.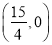
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲乙两地之间的距离为810米,小明和小天分别从甲乙两地出发,匀速相向而行,已知小明先出发1分钟后,小天再出发,两人在甲乙之间的丙地相遇,此时,小明发现有小学同学也在丙地,于是聊了一会儿,随后以原来速度的
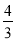 倍返回甲地,小天相遇后继续以原速向甲地前行,到达甲地后立即原速返回,直至再次与小明相遇.已知在整个过程中,小明、小天两人之间的距离
倍返回甲地,小天相遇后继续以原速向甲地前行,到达甲地后立即原速返回,直至再次与小明相遇.已知在整个过程中,小明、小天两人之间的距离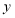 (米与小明出发的时间
(米与小明出发的时间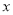 (分钟)之间的关系如图所示,则在第二次相遇时两人距离乙地______米.
(分钟)之间的关系如图所示,则在第二次相遇时两人距离乙地______米.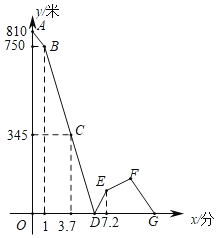
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角扳的一边交CD于点F.另一边交CB的延长线于点G.
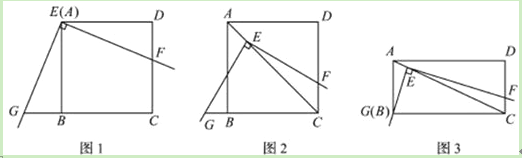
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求
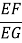 的值.
的值.
相关试题

