【题目】(本小题满分9分)已知点D是![]() 边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
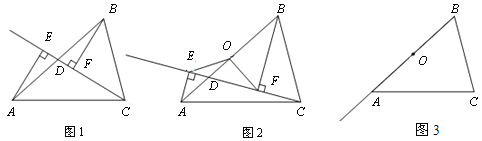
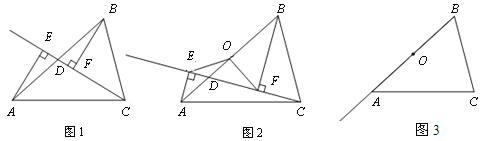
(1)如图1,当点D与点O重合时,AE与BF的位置关系是____________,OE与OF的数量关系是__________;
(2)如图2,当点D在线段AB上不与点O重合时,试判断OE与OF的数量关系,并给予证明;
(3)如图3,当点D在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.
参考答案:
【答案】(1)AE∥BF,OE=OF;(2) OE=OF,证明见解析;(3)(2)中的结论成立,图形及证明思路见解析.
【解析】(1)AE∥BF,OE=OF.
如图,
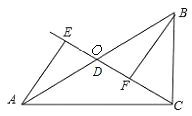
当点D与点O重合时,AE与BF的位置关系是AE∥BF,OE与OF的数量关系是OE=OF.
理由是:∵O为AB的中点,
∴AO=BO,
∵AE⊥CD,BF⊥CO,
∴AE∥BF,∠AEO=∠BFO=90°,(2分)
在![]() 和
和![]() 中
中
∠AOE=∠BOF,∠AEO=∠BFO,AO=BO,
∴△AEO≌△BFO,
∴OE=OF,
故答案为:AE∥BF,OE=OF(3分)
(2)结论:OE=OF. (4分)
证明:如图,延长EO交BF于G.

∵AE∥BF,
∴∠AEO=∠BGO,
在![]() 和
和![]() 中,
中,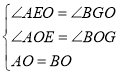 ,
,
∴△AEO≌△BGO(ASA).
∴OE=OG.
∵BF⊥CD,
∴FO是![]() 斜边上的中线,
斜边上的中线,
∴OE=OF=OG,
即OE=OF.(6分)
(3)(2)中的结论仍然成立. (7分)
所画图形如图所示,
 (8分)
(8分)
证明思路:延长EO、FB交于G.
由(2)的证明思路可以得到△AOE≌△BOG,由全等得到OE=OG;由BF⊥CD,得到FO是![]() 斜边GE上的中线;可得到OE=OF.(9分)
斜边GE上的中线;可得到OE=OF.(9分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)x2﹣4x=0
(2)x2﹣8x﹣10=0(配方法)
(3)x2+6x﹣1=0
(4)2x2+5x﹣3=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a是不等式2x﹣1>5的解,b不是不等式2x﹣1>5的解,则下列结论正确的是( )
A.a>b
B.a≥b
C.a<b
D.a≤b -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校随机抽查的20名八年级男生的身高统计表:
身高(cm)
150
155
160
163
165
168
人数(人)
1
3
4
4
5
3
这组数据的众数是__cm,中位数是__cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分9分)已知点D是
 边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.(1)如图1,当点D与点O重合时,AE与BF的位置关系是____________,OE与OF的数量关系是__________;
(2)如图2,当点D在线段AB上不与点O重合时,试判断OE与OF的数量关系,并给予证明;
(3)如图3,当点D在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路. (备注:直角三角形中,斜边上的中线等于斜边的一半)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ma2﹣4ma+4m= .
-
科目: 来源: 题型:
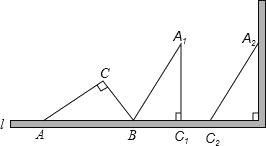
查看答案和解析>>【题目】如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
(1)请直接写出AB= ,AC= ;
(2)画出在搬动此物体的整个过程中A点所经过的路径,并求出该路径的长度.
(3)设O、H分别为边AB、AC的中点,在将△ABC绕点B顺时针方向翻转到△A1BC1的位置这一过程中,求线段OH所扫过部分的面积.
相关试题

