Question

【题目】过反比例函数（）图像上一动点M作MN⊥x轴交x轴于点N，Q是直线MN上一点，且MQ＝2MN，过点Q作QR∥轴交该反比例函数图像于点R，已知S△QRM=8，那么k的值为_____.

Answer 1

【答案】12或4

【解析】

由k>0，可知点M在第一象限或第三象限，设点M的坐标为（m，），分别讨论点Q所在象限，根据MQ＝2MN，用m、k表示出点Q和点R的坐标，利用S△QRM=8，即可得出k的值.

∵k>0，

∴点M在第一象限或第三象限，

点M在第一象限时，设点M的坐标为（m，），

①如图，当点Q在第一象限时，

∵MQ＝2MN，

∴QN=3MN，

∴点Q坐标为（m，），

∵QR//x轴，点R在反比例函数上，

∴点R坐标为（，），

∴QR=m-=，QM=-=，

∵S△QRM=8，

∴=8，

解得：k=12.

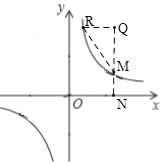
②如图，当点Q在第四象限时，

∵MQ＝2MN，

∴MN=NQ，

∴点Q坐标为（m，-），

∵QR//x轴，点R在反比例函数上，

∴点R坐标为（-m，-），

∴QR=m-(-m)=2m，QM=-（-）=，

∵∵S△QRM=8，

∴2m=8，

解得：k=4，

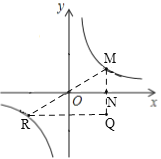
同理可得：点M在第三象限时k=4或k=12，

综上所述：k的值为12或4.

故答案为：12或4.