搜索
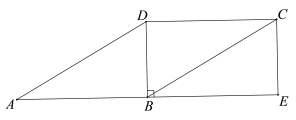
【题目】如图，在□ABCD中，∠ABD=90°，延长AB至点E，使BE=AB，连接CE．
（1）求证：四边形BECD是矩形；
（2）连接DE交BC于点F，连接AF，若CE=2，∠DAB=30°，求AF的长．
参考答案：
【答案】（1）见解析（2）
【解析】
（1）根据矩形的判定即可求解；
（2）根据题意作出图形，根据直角三角形的性质及勾股定理即可求解.
（1）∵四边形ABCD是平行四边形，
又BE=AB
∴四边形BECD是平行四边形，
∵∠ABD=90°，
∴平行四边形BECD是矩形；
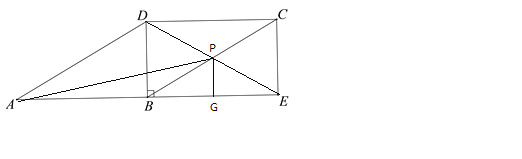
（2）如图,作PG⊥AE于G点，
∵CE=2，∠DAB=30°，
∴∠CBE=30°，PG=1，BE=2
∴AB=2
∵P为BC中点，∴G为BE中点，
∴AG=AB+BG=3
∴AP=
=
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形ABCD中,点0为正方形的中心,直线m经过点0,过A、B两点作直线m的垂线AE、BF,垂足分别为点E、F,若AE=2,BF=5,则EF长为____________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上有三个点A、B、C，完成系列问题：
（1）A、C两点间的距离是多少？
（2）在数轴上找到点D，使点D到B、C两点的距离相等；并在数轴上标出点D表示的数．
（3）若点E与B点的距离是5，求点E表示的数是什么？
（4）若点F与A点的距离是a（a>0），直接写出点F表示的数是多少？（用字母a表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某厂家在甲、乙两商场销售同一件商品所获得的利润分别为
，(单位：元)，与销售量
(单位：件)的函数关系图象如图所示，试根据图像解决下列问题：
(1)分别求出
关于的函数解析式；(2)现厂家分配该商品800件给甲商场、400件给乙商场，当甲、乙两商场售完这批商品后，厂家可获得总利润多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某餐厅中1张餐桌可坐6人，有以下两种摆放方式：
（1）对于方式一：4张桌子拼在一起可坐 人；对于方式二，n张桌子拼在一起可坐 人；
（2）该餐厅有40张这样的长方形桌子，若按方式一每5张拼成一张大桌子，则40张桌子可拼成8张大桌子，共可坐多少人？
（3）在（2）中，若改成每8张拼成一张大桌子，按方式二的拼法，则40张桌子共可坐多少人？
（4）一天中午，该餐厅来了98位顾客共同就餐，要求用满座位，但餐厅中只有25张这样的长方形桌子可用，若你是这家餐厅的经理，你打算选择哪种方式来摆餐桌呢（不考虑场地等因素）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2=a2+2ab+b2展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3=a3+3a2b+3ab2+b2展开式中的系数等等．
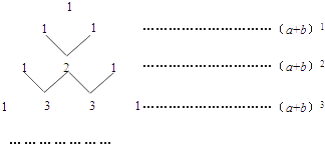
（1）根据上面的规律，则（a+b）5的展开式=________．
（2）利用上面的规律计算：25﹣5×24+10×23﹣10×22+5×2﹣1=________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,D为AB的中点,F为BC边上一点,连接CD、AF交干点E.若∠FAC=90°-3∠BAF,BF:AC=2:5,EF=2,则AB长为__________.
相关试题
