搜索
【题目】如图,在△ABC中,AC=BC,D为AB的中点,F为BC边上一点,连接CD、AF交干点E.若∠FAC=90°-3∠BAF,BF:AC=2:5,EF=2,则AB长为__________.
参考答案：
【答案】
【解析】解：如图，延长CD到H，使DH=DE，作FG∥AB交CD于G．∵AC=BC，AD=BD，∴CD⊥AB．∵DH=DE，CD⊥AB，∴AH=AE，∠HAD=∠EAD，∴∠HAE=2∠BAF．又∵∠FAC=90°-3∠BAF ，∠FAC+∠BAF+∠ACD=90°，∴∠ACD=2∠BAF=∠HAE．∵∠H=∠H，∠ACD=∠HAE，∴△HAE∽△HCA，∴AH：HE=HC：AH，∴AH2=HEHC．
又∵BF：AC=BF：BC=2：5，∴CF：BC=3：5．∵FG∥AB，∴FG：BD=CF：BC=3：5，FG：BD=FG：AD=EF：AE=EG：DE=3：5．又∵EF=2，∴AE=
，∴AH=
．∵DE：DG=5：8，∴DE=
GD=
×
CD=
CD，∴CD=4DE=4DH，∴
=2HD（HD+CD）=2HD5HD=10HD2，∴HD=
，∴DE=
．∵
=
，∴AD=
，∴AB=2AD=
．故答案为： 
．
-
科目： 来源： 题型：
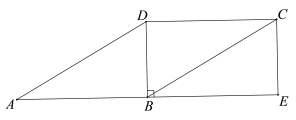
查看答案和解析>>【题目】如图，在□ABCD中，∠ABD=90°，延长AB至点E，使BE=AB，连接CE．
（1）求证：四边形BECD是矩形；
（2）连接DE交BC于点F，连接AF，若CE=2，∠DAB=30°，求AF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某餐厅中1张餐桌可坐6人，有以下两种摆放方式：
（1）对于方式一：4张桌子拼在一起可坐 人；对于方式二，n张桌子拼在一起可坐 人；
（2）该餐厅有40张这样的长方形桌子，若按方式一每5张拼成一张大桌子，则40张桌子可拼成8张大桌子，共可坐多少人？
（3）在（2）中，若改成每8张拼成一张大桌子，按方式二的拼法，则40张桌子共可坐多少人？
（4）一天中午，该餐厅来了98位顾客共同就餐，要求用满座位，但餐厅中只有25张这样的长方形桌子可用，若你是这家餐厅的经理，你打算选择哪种方式来摆餐桌呢（不考虑场地等因素）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2=a2+2ab+b2展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3=a3+3a2b+3ab2+b2展开式中的系数等等．
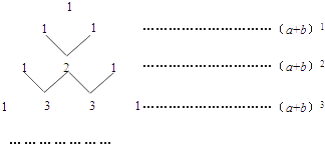
（1）根据上面的规律，则（a+b）5的展开式=________．
（2）利用上面的规律计算：25﹣5×24+10×23﹣10×22+5×2﹣1=________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。
(1)在图中画一个以AB为腰的等腰三角形△ABC，点C在小正方形的顶点上，且tan∠B=3；
(2)在图中画一个以AB为底的等腰三角形△ABD,点D在小正方形的项点上,且△ABD是锐角三角形.连接CD,请直接写出线段CD的长。
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着2018年两会的隆重召开,中学校园掀起了关注时事政治的热潮我区及时开展“做一个关心国家大事的中学生”主题活动。为了了解我区中学生获取时事新闻的主要途径，分别从电脑上网、手机上网、听广播、看电视、看报纸五个方面,在全区范围内随机抽取了若干名中学生进行问卷调查(每名中学生只选一种主要途径),根据调查结果绘制了如图所示的不完整的统计图请根据统计图的信息回答下列问题:
(1)本次调查共抽取了中学生多少人?
(2)求本次调查中,以听广播获取时事新闻为主要途径的人数并补全条形统计图；
(3)若本区共有中学生7000人，请你估计我区以看电视以看电视获取时事新闻为主要途径的中学生有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F，连接CF.
(1)如图1,求证:四边形ADCF是平行四边形；
(2)如图2.连接CE，在不添加任何助线的情况下,请直接写出图2中所有与△BEC面积相等的三角形。
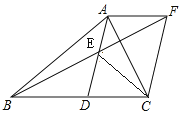
图1 图2
相关试题
