【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
![]()
(1)A、C两点间的距离是多少?
(2)在数轴上找到点D,使点D到B、C两点的距离相等;并在数轴上标出点D表示的数.
(3)若点E与B点的距离是5,求点E表示的数是什么?
(4)若点F与A点的距离是a(a>0),直接写出点F表示的数是多少?(用字母a表示)
参考答案:
【答案】(1)A、C两点之间的距离为5;(3)正确找到点D;点D表示的数是0;(3)点E表示的数为3或-7; (4)点F表示的数为:-3+a或-3-a.
【解析】
(1)根据数轴的性质即可求解;
(2)根据点D为B、C中点即可求解;
(3)根据数轴的性质分情况讨论即可求解;
(4)根据数轴上的点之间的距离的定义即可求解.
解:(1)2-(-3)=5.即A、C两点之间的距离为5;
(2)依题意得到点D为B、C中点
∴D表示的数是![]()
如图,D为所求;

(3)设E表示的数是x,则|x+2|=5,
解得x=3或x=-7.即点E表示的数为3或-7;
(4) 设F表示的数是y,则|y+3|=a
故y+3=±a
解y=-3+a或y=-3-a
故点F表示的数为:-3+a或-3-a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下图,解答下列问题.

(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?
(2)某一层上有65个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.同样,
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
由前五层的圆圈个数和得:1+3+5+7+9=52.…
根据上述请你计算:1+3+5+…+99的和
(4)猜测:从1开始的n个连续奇数之和是多少?用公式把它表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】刚刚升入初一,学习成绩优异但体育一般的王晴同学未雨绸缪,已经为将来的体育中考做起了准备.上周末她在家练习1分钟跳绳,以每分钟150下为基准,超过或不足的部分分别用正负数来表示,8次成绩(单位:下)分别是-10,-8,-5,-2,+2,+8,+3,-4.
(1)成绩最好的一次比最差的一次多跳多少下?
(2)求王晴这8次跳绳的平均成绩.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,点0为正方形的中心,直线m经过点0,过A、B两点作直线m的垂线AE、BF,垂足分别为点E、F,若AE=2,BF=5,则EF长为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家在甲、乙两商场销售同一件商品所获得的利润分别为
 ,(单位:元),
,(单位:元), 与销售量
与销售量 (单位:件)的函数关系图象如图所示,试根据图像解决下列问题:
(单位:件)的函数关系图象如图所示,试根据图像解决下列问题:
(1)分别求出
 关于
关于 的函数解析式;
的函数解析式;(2)现厂家分配该商品800件给甲商场、400件给乙商场,当甲、乙两商场售完这批商品后,厂家可获得总利润多少元?
-
科目: 来源: 题型:
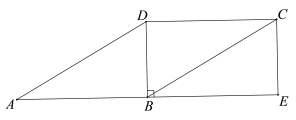
查看答案和解析>>【题目】如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中1张餐桌可坐6人,有以下两种摆放方式:
(1)对于方式一:4张桌子拼在一起可坐 人;对于方式二,n张桌子拼在一起可坐 人;
(2)该餐厅有40张这样的长方形桌子,若按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改成每8张拼成一张大桌子,按方式二的拼法,则40张桌子共可坐多少人?
(4)一天中午,该餐厅来了98位顾客共同就餐,要求用满座位,但餐厅中只有25张这样的长方形桌子可用,若你是这家餐厅的经理,你打算选择哪种方式来摆餐桌呢(不考虑场地等因素)?

相关试题

