【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC。
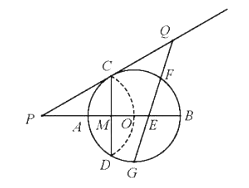
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合)。问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由。
参考答案:
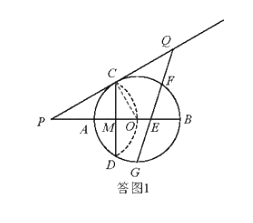
【答案】(1)2![]() ;(2)证明过程见解析;(3)定值为8.
;(2)证明过程见解析;(3)定值为8.
【解析】
试题分析:(1)连接OC,根据折叠图形的性质得出OM=1,根据勾股定理的性质得出CD的长度;(2)首先根据勾股定理求出PC的长度,然后根据勾股定理的逆定理得出切线;(3)连接GA、AF、GB,根据题意得出△AGE与△FGA相似,从而得出GE·GF=![]() ,然后根据等腰直角三角形的性质得出答案.
,然后根据等腰直角三角形的性质得出答案.
试题解析:(1)如答图1,连接OC ∵![]() 沿CD翻折后,A与O重合 ∴OM=
沿CD翻折后,A与O重合 ∴OM=![]() OA=1,CD⊥OA
OA=1,CD⊥OA
∵OC=2 ∴CD=2CM=2![]() =2
=2![]()
(2)∵PA=OA=2,AM=OM=1,CM=![]() 又∵
又∵![]() CMP=∠OMC=90° ∴PC=
CMP=∠OMC=90° ∴PC=![]() =2
=2![]()
∵OC=2,PO=4 ∴![]() ∴∠PCO=90° ∴PC与☉O相切
∴∠PCO=90° ∴PC与☉O相切
(3)GE·GF为定值,理由如下: 如答图2,连接GA、AF、GB ∵G为![]() 中点 ∴
中点 ∴![]()
∴∠BAG=∠AFG ∵∠AGE=∠FGA ∴△AGE∽△FGA ∴![]()
∴GE·GF=![]() ∵AB为直径,AB=4 ∴∠BAG=∠ABG=45° ∴AG=2
∵AB为直径,AB=4 ∴∠BAG=∠ABG=45° ∴AG=2![]() ∴GE·GF=
∴GE·GF=![]() =8
=8
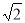
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
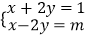 .
.
(1)求这个方程组的解;
(2)当m取何值时,这个方程组的解中,x大于1,y不小于﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,有矩形AOBC,点A、B的坐标分别为(0,4)、(10,0),点P的坐标为(2,0),点M在线段AO上,点N在线段AC上,总有∠MPN=90 ,点M从点O运动到点A,当点M运动到A点时,点N与点C重合(如图2)。令AM=x
(1).直接写出点C的坐标___________;
(2)、①设MN2=y,请写出y关于x的函数关系式,并求出y的最小值;
②连接AP交MN于点D,若MN⊥A P,求x的值;
(3)、当点M在边AO上运动时,∠PMN的大小是否发生变化?请说明理由.
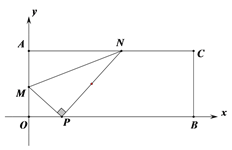
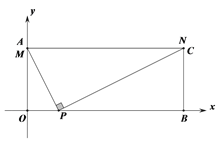
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形,
(1)设图1中阴影部分面积为S1 , 图2中阴影部分面积为S2 , 请直接用含a、b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.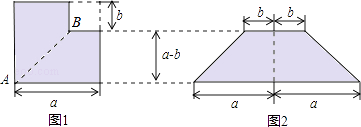
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解一批保温瓶的保温性能,从中抽取了10只保温瓶进行试验.在这个问题中,样本是______________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学表达式:(1)﹣3<0(2)3x+5>0(3)x2﹣6(4)x=﹣2(5)y≠0(6)x≥50中,不等式的个数是()
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
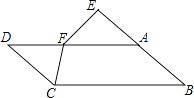
查看答案和解析>>【题目】如图:在平行四边形ABCD中,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证:CF=EF.
相关试题

