【题目】如图,在ABCD中,点E到AD,AB,BC三边的距离都相等,则∠AEB( )
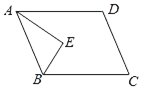
A.是锐角B.是直角C.是钝角D.度数不确定
参考答案:
【答案】B
【解析】
由平行四边形的性质得出∠BAD+∠ABC=180°,由题意得出AE平分∠BAD,BE平分∠ABC,得出∠BAE=![]() ∠BAD,∠ABE=
∠BAD,∠ABE=![]() ∠ABC,求出∠BAE+∠ABE=
∠ABC,求出∠BAE+∠ABE=![]() (BAD+∠ABC)=90°,再由三角形内角和定理即可得出结果.
(BAD+∠ABC)=90°,再由三角形内角和定理即可得出结果.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BAD+∠ABC=180°,
∵点E到AD,AB,BC三边的距离都相等,
∴AE平分∠BAD,BE平分∠ABC,
∴∠BAE=![]() ∠BAD,∠ABE=
∠BAD,∠ABE=![]() ∠ABC,
∠ABC,
∴∠BAE+∠ABE=![]() (BAD+∠ABC)=
(BAD+∠ABC)=![]() ×180°=90°,
×180°=90°,
∴∠AEB=90°;
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2012年8月份的日历. 我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减,例如:
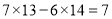 ,
, ,不难发现,结果都是7.
,不难发现,结果都是7. (1)请你再选择两个类似的部分试一试,看看是否符合这个规律;
(2)请你利用整式的运算对以上的规律加以证明.
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线
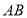 交
交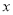 轴于点
轴于点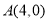 ,交
,交 轴于点
轴于点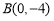 .
.(1)如图①,若
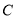 的坐标为
的坐标为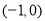 ,且
,且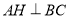 于点
于点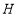 ,
,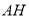 交
交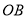 于点
于点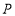 ,试求点
,试求点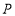 的坐标;
的坐标;(2)如图②,在(I)的条件下,连接
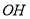 ,求
,求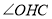 的度数;
的度数;(3)如图③,若点
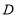 为
为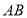 的中点,点
的中点,点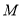 为
为 轴正半轴上一动点,连接
轴正半轴上一动点,连接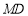 ,过
,过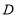 作
作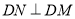 交
交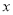 轴于
轴于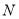 点,当
点,当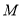 点在
点在 轴正半轴上运动的过程中,式子
轴正半轴上运动的过程中,式子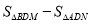 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值. 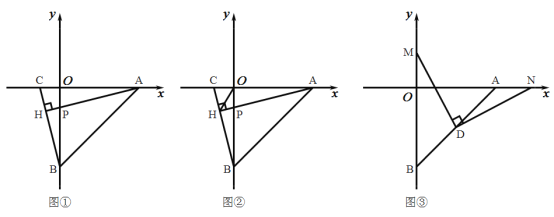
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明想本周末去看电影,爸爸建议通过一个游戏决定小明能否去,规则为:在一个不透明的盒子中放入三张卡片,每张卡片上写着一个实数,分别为
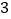 ,
, ,
,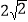 (每张卡片除了上面的实数不同以外其余均相同).爸爸让小明从中随机取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.
(每张卡片除了上面的实数不同以外其余均相同).爸爸让小明从中随机取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.(1)请你直接写出按照爸爸的规则小明能去看电影的概率;
(2)小明想了想,和爸爸重新约定游戏规则,自己从盒子中随机抽取两次,每次随机抽取一张卡片,第一次抽取后记下卡片上的数,再将卡片放回盒中抽取第二次,如果抽取的两数之积是有理数,自己就去,否则就不去,请你用列表或树状图法求出按照此规则小明本周末能看电影的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1, 将Cl绕点B中心对称变换得C2, C2与x轴交于另一点C,将C2绕点C中心对称变换得C3, 连接C与C3的顶点,则图中阴影部分的面积为( )
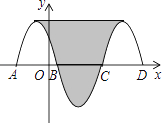
A. 32 B. 24 C. 36 D. 48
-
科目: 来源: 题型:
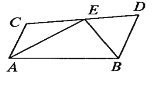
查看答案和解析>>【题目】如图,
 分别平分
分别平分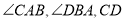 经过点
经过点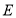 ,则
,则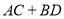 ( )
( )
A.
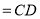 B.
B.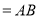 C.
C.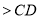 D.
D.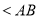
-
科目: 来源: 题型:
查看答案和解析>>【题目】维修一项工程,甲、乙两队合做,
 天能完成,共付工钱
天能完成,共付工钱 元,甲队每天的工钱比乙队多
元,甲队每天的工钱比乙队多 元.若两队独做,乙队工期是甲队的
元.若两队独做,乙队工期是甲队的 倍.
倍.(1)甲、乙两队独做各需多少天完成?
(2)若两队独做,哪队工钱总额较少?
相关试题

