【题目】某超市决定购进甲、乙两种取暖器,已知甲种取暖器每台进价比乙种取暖器多500元, 用40000元购进甲种取暖器的数量与用30000元购进乙种取暖器的数量相同.请解答下列问题:
(1)求甲、乙两种取暖器每台的进价;
(2)若甲种取暖器每台售价2500元,乙种取暖器每台售价1800元,超市欲同时购进两种取暖器20 台,且全部售出.设购进甲种取暖器x(台),所获利润为y(元),试用关于x的式子表示y;
(3)在(2)的条件下,若超市计划用不超过36000元购进取暖器,且甲种取暖器至少购进10台, 并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器. 求购买按摩器的方案.
参考答案:
【答案】(1)甲、乙两种取暖器每台进价分别为2000元、1500元;(2)y=200x+6000;(3)有两种购买方案:①A型0台,B型12台;②A型7台,B型1台.
【解析】
(1)根据题意可以列出相应的方程,从而可以分别求得甲、乙两种取暖器每台的进价,注意分式方程要检验;
(2)根据题意和(1)中的答案可以得到所获利润y(元)与甲种取暖器x(台)之间的函数关系式;
(3)设购买甲种取暖器n台,根据商场计划用不超过36000元购进取暖器共20台,可以求得n的取值范围,从而可以求得所能获得的最大利润,然后根据题意列出二元一次方程,找到符合题意的解即可.
解:(1)设乙种取暖器每台进价为x元,则甲种取暖器每台进价为(x+500)元.
根据题意得:![]() ,
,
解得:x=1500
经检验x=1500是分式方程的解,且x+500=2000,
即甲、乙两种取暖器每台进价分别为2000元、1500元;
(2)根据题意得:y=(25002000)x+(18001500)(20x)=200x+6000;
(3)设购买甲种取暖器n台,则购买乙种取暖器(20n)台.
根据题意得:2000n+1500(20n)≤36000,且n≥10(n为正整数)
解得:10≤n≤12
当n=12时,最大利润为8400元
设购买A型按摩器a台,购买B型按摩器b台,则1100a+700b=8400,
故有两种购买方案:①A型0台,B型12台;②A型7台,B型1台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某新型节能环保汽车油箱中原有汽油100升,汽车每行驶50千米耗油8升,试写出汽车行驶的路程x(千米)与油箱中剩余油量y(升)之间的函数关系式,并画出这个函数的图象,函数的图象是什么形状?
-
科目: 来源: 题型:
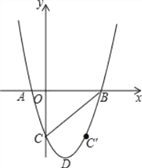
查看答案和解析>>【题目】已知抛物线y=x2﹣4x﹣m(m>0)与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,C点关于抛物线对称轴的对称点为C′点.
(1)若m=5时,求△ABD的面积.
(2)若在(1)的条件下,点E在线段BC下方的抛物线上运动,求△BCE面积的最大值.
(3)写出C点( , )、C′点( , )坐标(用含m的代数式表示)
如果点Q在抛物线的对称轴上,点P在抛物线上,以点C、C′、P、Q为顶点的四边形是平行四边形,直接写出Q点和P点的坐标(可用含m的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成
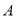 、
、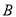 、
、 、
、 、
、 共
共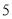 个区,
个区, 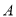 区是边长为
区是边长为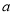 的正方形,
的正方形, 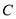 区是边长为
区是边长为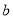 的正方形.
的正方形.(1)列式表示每个
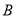 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果
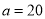 ,
, 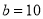 ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.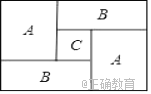
-
科目: 来源: 题型:
查看答案和解析>>【题目】考试前夕,为“连粽连中”的吉祥寓意,某校食堂购进甲、乙两种粽子520个,其中甲种粽子花费600元,乙种粽子花费800元,已知甲种粽子单价比乙种粽子单价高20%,乙种粽子的单价是多少元?甲、乙两种粽子各购买了多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
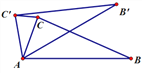
A. 70° B. 35° C. 40° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=
 ,⑤S△DOC=S四边形EOFB中,正确的有( )
,⑤S△DOC=S四边形EOFB中,正确的有( )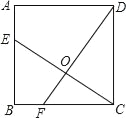
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

