【题目】某新型节能环保汽车油箱中原有汽油100升,汽车每行驶50千米耗油8升,试写出汽车行驶的路程x(千米)与油箱中剩余油量y(升)之间的函数关系式,并画出这个函数的图象,函数的图象是什么形状?
参考答案:
【答案】![]() ,见解析.
,见解析.
【解析】
由于汽车每行驶50千米耗油8升,那么汽车行驶路程x千米耗油![]() ,而汽车油箱中能盛汽油100升,由此即可确定加满油后,油箱中剩余油量y(升)与汽车行驶路程x(千米)之间的函数关系式.再画出函数图象即可解决问题.
,而汽车油箱中能盛汽油100升,由此即可确定加满油后,油箱中剩余油量y(升)与汽车行驶路程x(千米)之间的函数关系式.再画出函数图象即可解决问题.
∵汽车每行驶50千米耗油8升,
∴汽车行驶路程x千米耗油![]() ,
,
∴油箱中剩余油量y(升)与汽车行驶路程x(千米)之间的函数关系式是y=100-![]() .
.
∵![]() ,
,
∴![]() .
.
又∵路程x不能为负数,故![]() .
.
图象如图所示,
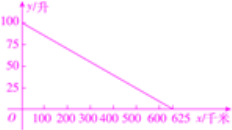
此时的图象为一条线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读第①小题的计算方法,再计算第②小题.
①–5
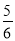 +(–9
+(–9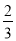 )+17
)+17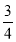 +(–3
+(–3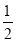 )
)解:原式=[(–5)+(–
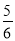 )]+[(–9)+(–
)]+[(–9)+(–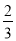 )]+(17+
)]+(17+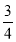 )+[(–3+(–
)+[(–3+(–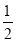 )]
)]=[(–5)+(–9)+(–3)+17]+[(–
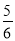 )+(–
)+(–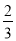 )+(–
)+(–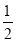 )+
)+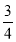 ]
]=0+(–1
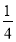 )
)=–1
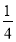 .
.上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000
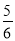 )+(﹣1999
)+(﹣1999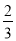 )+4000
)+4000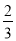 +(﹣1
+(﹣1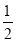 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】画出直线
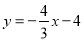 的图象,并解答下列问题:
的图象,并解答下列问题:(1)设它的图象与y轴、x轴分别交于点A、B,求AB的长;
(2)求
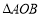 的周长(O为坐标原点);
的周长(O为坐标原点);(3)求点O到直线AB的距离;
(4)求
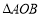 的面积.
的面积. -
科目: 来源: 题型:
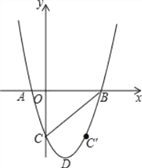
查看答案和解析>>【题目】已知抛物线y=x2﹣4x﹣m(m>0)与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,C点关于抛物线对称轴的对称点为C′点.
(1)若m=5时,求△ABD的面积.
(2)若在(1)的条件下,点E在线段BC下方的抛物线上运动,求△BCE面积的最大值.
(3)写出C点( , )、C′点( , )坐标(用含m的代数式表示)
如果点Q在抛物线的对称轴上,点P在抛物线上,以点C、C′、P、Q为顶点的四边形是平行四边形,直接写出Q点和P点的坐标(可用含m的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成
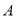 、
、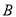 、
、 、
、 、
、 共
共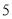 个区,
个区, 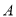 区是边长为
区是边长为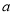 的正方形,
的正方形, 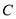 区是边长为
区是边长为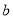 的正方形.
的正方形.(1)列式表示每个
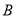 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果
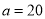 ,
, 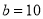 ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.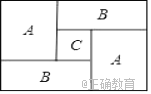
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市决定购进甲、乙两种取暖器,已知甲种取暖器每台进价比乙种取暖器多500元, 用40000元购进甲种取暖器的数量与用30000元购进乙种取暖器的数量相同.请解答下列问题:
(1)求甲、乙两种取暖器每台的进价;
(2)若甲种取暖器每台售价2500元,乙种取暖器每台售价1800元,超市欲同时购进两种取暖器20 台,且全部售出.设购进甲种取暖器x(台),所获利润为y(元),试用关于x的式子表示y;
(3)在(2)的条件下,若超市计划用不超过36000元购进取暖器,且甲种取暖器至少购进10台, 并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器. 求购买按摩器的方案.
相关试题

