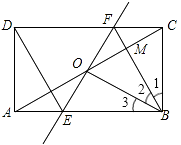
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( ) 
A.4个
B.3个
C.2个
D.1个
参考答案:
【答案】B
【解析】解:①∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
故①正确;
②∵△BOC为等边三角形,FO=FC,
∴BO⊥EF,BF⊥OC,
∴∠CMB=∠EOB=90°,
∴BO≠BM,
∴△EOB与△CMB不全等;
故②错误;
③易知△ADE≌△CBF,∠1=∠2=∠3=30°,
∴∠ADE=∠CBF=30°,∠BEO=60°,
∴∠CDE=60°,∠DFE=∠BEO=60°,
∴∠CDE=∠DFE,
∴DE=EF,
故③正确;
④易知△AOE≌△COF,
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∴S△AOE:S△BCM=2S△CMF:S△BCM= ![]() ,
,
∵∠FCO=30°,
∴FM= ![]() ,BM=
,BM= ![]() CM,
CM,
∴ ![]() =
= ![]() ,
,
∴S△AOE:S△BCM=2:3,
故④正确;
所以其中正确结论的个数为3个;
故选B
①利用线段垂直平分线的性质的逆定理可得结论;②在△EOB和△CMB中,对应直角边不相等,则两三角形不全等;③可证明∠CDE=∠DFE;④可通过面积转化进行解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解.
(1)ax2-2axy+ay2 (2)(2x+y)2﹣(x+2y)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形一边长为3,周长为15,则它的腰长等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S2017的值为( )

A.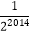
B.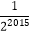
C.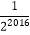
D.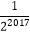
-
科目: 来源: 题型:
查看答案和解析>>【题目】长度分别为3cm,5cm,7cm,9cm的四根木棒,能搭成(首尾连结)三角形的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某颗粒物的直径是0.0000025,把0.0000025用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.
根据以上情况,请你回答下列问题:
(1)假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?
(2)若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.
相关试题

