【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径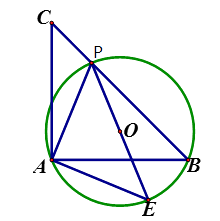
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
参考答案:
【答案】
(1)
证明:∵△ABC是等腰直角三角形,
∴∠C=∠ABC=45°,
∴∠PEA=∠ABC=45°
又∵PE是⊙O的直径,
∴∠PAE=90°,
∴∠PEA=∠APE=45°,
∴ △APE是等腰直角三角形.
(2)
解:∵△ABC是等腰直角三角形,
∴AC=AB,
同理AP=AE,
又∵∠CAB=∠PAE=90°,
∴∠CAP=∠BAE,
∴△CPA≌△BAE,
∴CP=BE,
在Rt△BPE中,∠PBE=90°,PE=2,
∴PB2+BE2=PE2,
∴CP2+PB2=PE2=4.
【解析】(1)根据等腰直角三角形性质得出∠C=∠ABC=∠PEA=45°,再由PE是⊙O的直径,得出∠PAE=90°,∠PEA=∠APE=45°,从而得证.
(2)根据题意可知,AC=AB,AP=AE,再证△CPA≌△BAE,得出CP=BE,依勾股定理即可得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。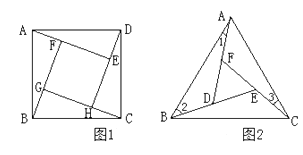
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设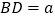 ,
, 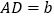 ,
, 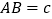 ,请探索
,请探索 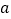 ,
, 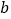 ,
, 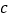 满足的等量关系。
满足的等量关系。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
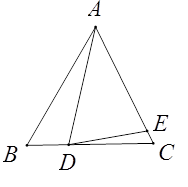
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之间的关系式.
(2)是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.

(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.

(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )

A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
相关试题

