【题目】综合题
(1)如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求:∠ABF的度数.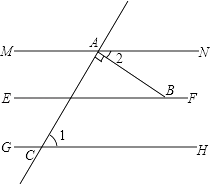
(2)计算: ![]() +
+ ![]() +|
+| ![]() ﹣2|﹣2.
﹣2|﹣2.
参考答案:
【答案】
(1)解:∵MN∥EF,GH∥EF,
∴MN∥GH,
∵∠1=70°,∠CAB=90°,
∴∠2=180°﹣∠1﹣∠CAB=20°,
∴∠ABF=180°﹣∠2=160°
(2)解:原式= ![]() ﹣
﹣ ![]() +2﹣
+2﹣ ![]() ﹣2
﹣2
=﹣ ![]()
【解析】利用平行线的性质及角的和差关系.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握实数的运算(先算乘方、开方,再算乘除,最后算加减,如果有括号,先算括号里面的,若没有括号,在同一级运算中,要从左到右进行运算)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12,10,6,8,则第5组的百分比是( )
A. 10% B. 20% C. 30% D. 40%
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=2(x-1)2+3上的三个点,则y1,y2,y3的大小关系是( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
-
科目: 来源: 题型:
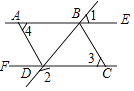
查看答案和解析>>【题目】如图,DA是∠BDF的平分线,∠3=∠4,若∠1=40°,∠2=140°,则∠CBD的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的证明过程,在每步后的横线上填写该步推理的依据. 如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB
证明:∵BE是∠ABC的角平分线
∴∠1=∠2
又∵∠E=∠1
∴∠E=∠2
∴AE∥BC
∴∠A+∠ABC=180°
又∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB .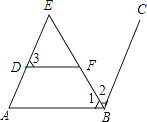
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(1,-2)关于x轴对称的点的坐标是( )
A. (1,-2) B. (-1,2) C. (-1,-2) D. (1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
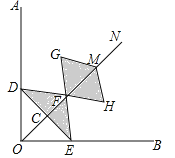
A.
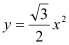 B.
B.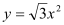 C.
C. D.
D.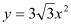
相关试题

