【题目】如图:在六边形ABCDEF中,AF∥CD,AB∥DE,∠BAF=100°,∠BCD=120°.
求∠ABC和∠D的度数.

参考答案:
【答案】∠CDE=100°;∠ABC=140°.
【解析】
连接AD,由AF∥CD得出∠FAD=∠ADC,由AB∥DE得出∠BAD=∠ADE,故可得出∠CDE=∠BAF=100°,∠FAD+∠BAD=∠ADC+∠BAD=100°,再由四边形内角和定理即可得出∠ABC的度数.
解:连接AD
∵AF∥CD,AB∥DE,
∴∠FAD=∠ADC,∠BAD=∠ADE,
∴∠BAF=∠CDE=100°
∵∠ABC+∠DCB+∠BAD+∠ADC=360°,
又∵∠FAB=∠FAD+∠BAD=∠ADC+∠BAD=100°,
∴∠ABC=360°-120°-100°=140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A.在直角三角形中,两条边的平方和等于第三边的平方
B.如果一个三角形两边的平方差等于第三边的平方,那么这个三角形是直角三角形
C.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a2+b2=c2,则∠A=90°
D.在△ABC中,若a=3,b=4,则c=5
-
科目: 来源: 题型:
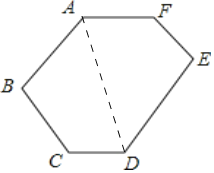
查看答案和解析>>【题目】如图,在ABC中,高AD、BE相交于点O,AE=BE,BC=5,且BD=
 CD.
CD.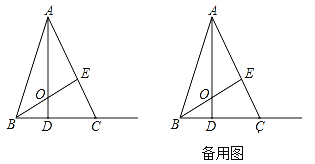
(1)①求证:△AOE≌△BCE;②求线段AO的长.
(2)动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,△POQ的面积为S,请用含t的式子表示S,并直接写出t相应的的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
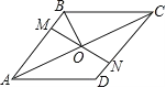
A.28°B.56°C.62°D.72°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取900°;而乙同学说,θ也能取800°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
相关试题

