【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.

参考答案:
【答案】(Ⅰ)AC =8;BD=CD=5![]() ;(Ⅱ)BD=5.
;(Ⅱ)BD=5.
【解析】试题分析:(1)、根据直径得出∠CAB=∠BDC=90°,然后根据Rt△CAB的勾股定理得出AC的长度,然后根据等腰直角△BDC求出BD和CD的长度;(2)、连接OB,OD,根据AD平分∠CAB,且∠CAB=60°得出∠DOB=2∠DAB=60°,从而得出△OBD为等边三角形,从而得出BD的长度.
试题解析:(1)、如图①,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6, ∴由勾股定理得到:AC=![]() =
=![]() =8.
=8.
∵AD平分∠CAB, ∴![]() =
=![]() ,∴CD=BD.
,∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,∴易求BD=CD=5![]() ;
;
(2)、如图②,连接OB,OD. ∵AD平分∠CAB,且∠CAB=60°,∴∠DAB=![]() ∠CAB=30°,∴∠DOB=2∠DAB=60°.
∠CAB=30°,∴∠DOB=2∠DAB=60°.
又∵OB=OD,∴△OBD是等边三角形,∴BD=OB=OD.∵⊙O的直径为10,则OB=5, ∴BD=5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行团上午6时从旅馆出发,乘汽车到距离210km的著名旅游景点游玩,已知该汽车离旅馆的距离S(km)与时间t(h)的关系如图所示,根据图像提供的信息,解答以下问题:

(1)求该旅行团在景点游玩了多少小时?
(2)求该旅行团去景点的平均速度?
(3)求返回宾馆时该汽车离旅馆的距离S(km)与时间t(h)的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A.在直角三角形中,两条边的平方和等于第三边的平方
B.如果一个三角形两边的平方差等于第三边的平方,那么这个三角形是直角三角形
C.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a2+b2=c2,则∠A=90°
D.在△ABC中,若a=3,b=4,则c=5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABC中,高AD、BE相交于点O,AE=BE,BC=5,且BD=
 CD.
CD.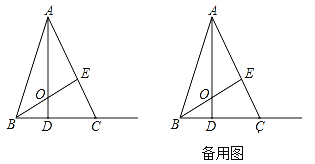
(1)①求证:△AOE≌△BCE;②求线段AO的长.
(2)动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,△POQ的面积为S,请用含t的式子表示S,并直接写出t相应的的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在六边形ABCDEF中,AF∥CD,AB∥DE,∠BAF=100°,∠BCD=120°.
求∠ABC和∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
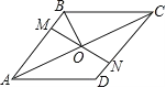
A.28°B.56°C.62°D.72°
相关试题

