【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,以
,以![]() 为边在数轴的上方作正方形ABCD.动点
为边在数轴的上方作正方形ABCD.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴正方向匀速运动,同时动点
个单位长度的速度沿数轴正方向匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,到达
匀速运动,到达![]() 点后再以同样的速度沿数轴正方向匀速运动,设运动时间为
点后再以同样的速度沿数轴正方向匀速运动,设运动时间为![]() 秒
秒![]() .
.
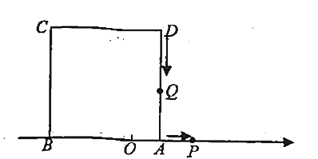
(1)若点![]() 在线段
在线段![]() .上运动,当t为何值时,
.上运动,当t为何值时,![]() ?
?
(2)若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,当t为何值时,三角形
,当t为何值时,三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的
面积的![]() ?
?
(3)在点![]() 和点
和点![]() 运动的过程中,当
运动的过程中,当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 恰好重合?
恰好重合?
(4)当点![]() 在数轴上运动时,是否存在某-时刻t,使得线段
在数轴上运动时,是否存在某-时刻t,使得线段![]() 的长为
的长为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)4;(4)存在,t=3或5,理由见详解.
;(3)4;(4)存在,t=3或5,理由见详解.
【解析】
(1)由数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,以
,以![]() 为边在数轴的上方作正方形ABCD,
为边在数轴的上方作正方形ABCD,![]() ,列出方程,即可求解;
,列出方程,即可求解;
(2)根据三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的
面积的![]() ,列出方程,即可;
,列出方程,即可;
(3)根据等量关系,列出方程即可求解;
(4)分两种情况:①当点Q在点P的左侧时, ②当点Q在点P的右侧时,分别列出方程,即可求解.
(1)∵数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,以
,以![]() 为边在数轴的上方作正方形ABCD,
为边在数轴的上方作正方形ABCD,
∴AD=AB=4,
∴AQ=4-2t,AP=t,
∵![]() ,
,
∴4-2t =t,解得:t=![]() ,
,
∴当t=![]() 秒时,
秒时,![]() ;
;
(2)∵AQ=4-2t,AB=4,
∴![]() ,正方形
,正方形![]() 面积=4×4=16,
面积=4×4=16,
∴8-4t=![]() ,解得:t=
,解得:t=![]() ,
,
∴当t=![]() 秒时,三角形
秒时,三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的
面积的![]() ;
;
(3)根据题意得:2t-4=t,解得:t=4,
∴当t=4秒时,点![]() 与点
与点![]() 恰好重合;
恰好重合;
(4)①当点Q在点P的左侧时,t-(2t-4)=1,解得:t=3,
②当点Q在点P的右侧时,(2t-4)-t=1,解得:t=5,
∴当t=3秒或5秒时,线段![]() 的长为
的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题12分)如图1,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t的式子表示AE、AD的长;
(2)如图2,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)连接DE,当t为何值时,△DEF为直角三角形?
(4)如图3,连接DE,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形AEA′D为菱形?
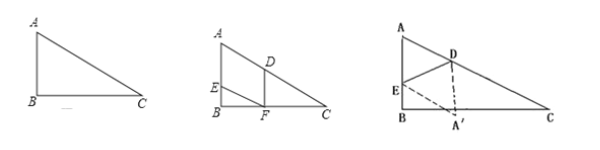
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.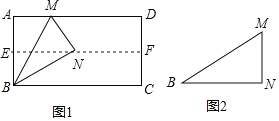
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
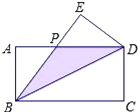
(1)求BD长度;(2)求点P到BD的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.
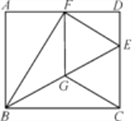
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上.向内放入两个半径为5 cm的钢球,测得上面一个钢球的最高点到底面的距离DC=16 cm(钢管的轴截面如图所示),则钢管的内径AD的长为_______cm.
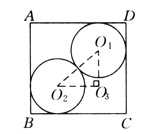
相关试题

