【题目】如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
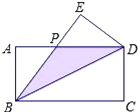
(1)求BD长度;(2)求点P到BD的距离.
参考答案:
【答案】(1)BD=2![]() ;(2)点P到BD的距离为
;(2)点P到BD的距离为![]() .
.
【解析】
(1)由勾股定理直接得出;
(2)设AP=x,证出△ABP≌△EDP,可知EP=x,PD=8﹣x,根据翻折不变性,可知ED=DC=AB=2,然后在Rt△PED中,利用勾股定理求出x,再由三角形的面积即可求出结论.
(1)∵四边形ABCD是长方形,
∴∠C=90°,CD=AB=2,
∴BD=![]() =2
=2![]() ;
;
(2)在△APB与△DEP中,
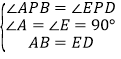 ,
,
∴△APB≌△DEP,
∴AP=EP,
设AP=x,则EP=x,PD=4﹣x,
∴在Rt△PED中,
x2+22=(4﹣x)2,
解得x=![]() ,
,
即AP=![]() ,
,
∴PD=4﹣![]() =
=![]() ,
,
设点P到BD的距离为h,
则S△BDP=![]() ,
,
解得:h=![]() ,
,
即点P到BD的距离为![]() .
.
-
科目: 来源: 题型:
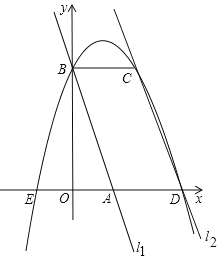
查看答案和解析>>【题目】如图,在平面直角坐标系中两条直线为l1:y=–3x+3,l2:y=–3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
①a–b+c=0;
②2a+b+c=5;
③抛物线关于直线x=1对称;
④抛物线过点(b,c);
⑤S四边形ABCD=5;
其中正确的个数有( )
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
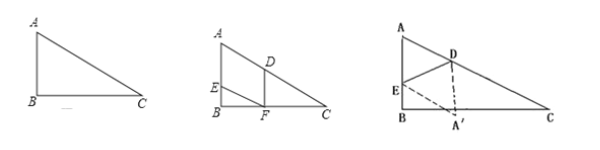
查看答案和解析>>【题目】(本小题12分)如图1,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t的式子表示AE、AD的长;
(2)如图2,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)连接DE,当t为何值时,△DEF为直角三角形?
(4)如图3,连接DE,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形AEA′D为菱形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.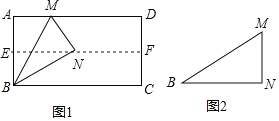
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点
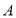 表示的数为
表示的数为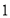 ,点
,点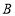 表示的数为
表示的数为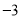 ,以
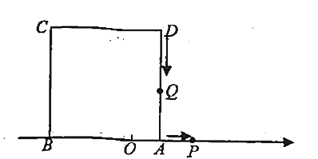
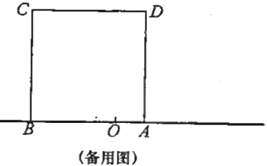
,以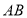 为边在数轴的上方作正方形ABCD.动点
为边在数轴的上方作正方形ABCD.动点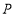 从点
从点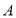 出发,以每秒
出发,以每秒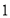 个单位长度的速度沿数轴正方向匀速运动,同时动点
个单位长度的速度沿数轴正方向匀速运动,同时动点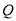 从点
从点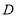 出发,以每秒
出发,以每秒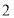 个单位长度的速度向点
个单位长度的速度向点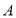 匀速运动,到达
匀速运动,到达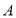 点后再以同样的速度沿数轴正方向匀速运动,设运动时间为
点后再以同样的速度沿数轴正方向匀速运动,设运动时间为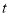 秒
秒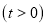 .
.
(1)若点
 在线段
在线段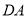 .上运动,当t为何值时,
.上运动,当t为何值时,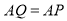 ?
?(2)若点
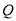 在线段
在线段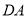 上运动,连接
上运动,连接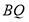 ,当t为何值时,三角形
,当t为何值时,三角形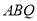 的面积等于正方形
的面积等于正方形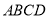 面积的
面积的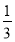 ?
?(3)在点
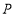 和点
和点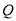 运动的过程中,当
运动的过程中,当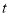 为何值时,点
为何值时,点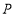 与点
与点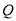 恰好重合?
恰好重合?(4)当点
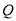 在数轴上运动时,是否存在某-时刻t,使得线段
在数轴上运动时,是否存在某-时刻t,使得线段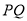 的长为
的长为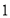 ,若存在,求出
,若存在,求出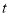 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
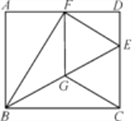
查看答案和解析>>【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.

相关试题

