搜索
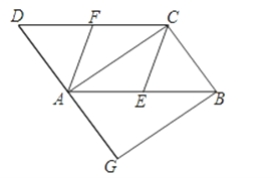
【题目】如图，在ABCD中，E、F分别为边AB、CD的中点，AC是对角线，过点B作BG∥AC交DA的延长线于点G．
（1）求证：CE∥AF；
（2）若∠G=90°，求证：四边形CEAF是菱形．
参考答案：
【答案】（1）见解析；（2）见解析
【解析】试题分析：（1）根据已知条件证明AE=CF，AE∥CF，从而得出四边形DFBE是平行四边形，即可证明CE∥AF；
（2）先证明CE=AE，再根据邻边相等的平行四边形是菱形，从而得出结论．
试题解析：（1）在□ABCD中，AB∥CD，AB=CD，
∵E、F分别为边AB、CD的中点，
∴CF=
CD，AE=
AB，
∴CF∥AE，CF=AE，
∴四边形CEAF为平行四边形，
∴CE∥AF；
（2）∵BG∥AC，
∴∠G=∠DAC=90°，
∴△DAC为直角三角形，
又∵F为边CD的中点，
∴AF=
CD=CF，
又∵四边形CEAF为平行四边形，
∴四边形CEAF为菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=22，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．
（1）数轴上点B表示的数 ；点P表示的数 （用含t的代数式表示）
（2）若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是 ．
（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2？
（4）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的有_______________(请填写所有正确结论的序号)
①在一个装有2白球和3个红球的袋中摸3个球，摸到红球是必然事件．②若
，则
； ③已知反比例函数
，若
，则
； ④分式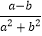
是最简分式 ； ⑤
和
是同类二次根式； -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
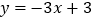与x轴交于点B，与y轴交于点A，以线段AB为边，在第一象限内作正方形ABCD，点C落在双曲线
（
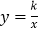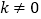）上，将正方形ABCD沿x轴负方向平移a个单位长度，使点D恰好落在双曲线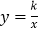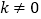（）上的点D1处，则a= ．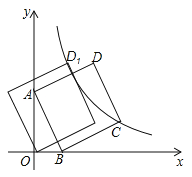
-
科目： 来源： 题型：
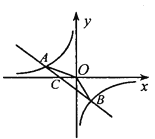
查看答案和解析>>【题目】如图，已知A(-4，n)，B(2，-4)是一次函数
的图像和反比例函数
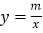的图像的两个交点．(1)求反比例函数和一次函数的解析式；
(2)求不等式
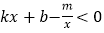的解集_________(请直接写出答案)．(3)求△AOB的面积；
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校要举办一次演讲比赛，每班只能选一人参加比赛．但八年级一班共有甲、乙两人的演讲水平相不相上下，现要在他们两人中选一人去参加全校的演讲比赛，经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛（胜者参赛）． 游戏规则如下：在两个不透明的盒子中，一个盒子里放着两个红球，一个白球；另一个盒子里放着三个白球，一个红球，从两个盒子中各摸一个球，若摸得的两个球都是红球，甲胜；摸得的两个球都是白球，乙胜，否则，视为平局．若为平局，继续上述游戏，直至分出胜负为止．
根据上述规则回答下列问题：
（1）从两个盒子各摸出一个球，一个球为白球，一个球为红球的概率是多少？
（2）该游戏公平吗？请用列表或树状图等方法说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，BC为⊙O的直径，A为圆上一点，点F为
的中点，延长AB、AC，与过F点的切线交于D、E两点． 
（1）求证：BC∥DE；
（2）若BC：DF=4：3，求tan∠ABC的值．
相关试题
