【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数 ;点P表示的数 (用含t的代数式表示)
(2)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是 .
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?
(4)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
![]()
参考答案:
【答案】(1)﹣14,8﹣5t;(2)11;(3)若点P、Q同时出发,2.5或3秒时P、Q之间的距离恰好等于2;(4)点P运动11秒时追上点Q.
【解析】
(1)根据已知可得B点表示的数为8-22;点P表示的数为8-5t;(2)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时两种情况求MN的长即可;(3)点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2,分①点P、Q相遇之前和②点P、Q相遇之后两种情况列方程求解即可;(4)点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据AC-BC=AB,列出方程求解即可.
(1)∵点A表示的数为8,B在A点左边,AB=22,
∴点B表示的数是8﹣22=﹣14,
∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
∴点P表示的数是8﹣5t.
(2)①当点P在点A、B两点之间运动时:
![]()
MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() (AP+BP)=
(AP+BP)=![]() AB=
AB=![]() ×22=11,
×22=11,
②当点P运动到点B的左侧时:
![]()
MN=MP﹣NP=![]() AP﹣
AP﹣![]() BP=
BP=![]() (AP﹣BP)=
(AP﹣BP)=![]() AB=11,
AB=11,
∴线段MN的长度不发生变化,其值为11.
(3)若点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
由题意得3t+2+5t=22,解得t=2.5;
②点P、Q相遇之后,
由题意得3t﹣2+5t=22,解得t=3.
答:若点P、Q同时出发,2.5或3秒时P、Q之间的距离恰好等于2;
(4)设点P运动x秒时,在点C处追上点Q,
![]()
则AC=5x,BC=3x,
∵AC﹣BC=AB,
∴5x﹣3x=22,
解得:x=11,
∴点P运动11秒时追上点Q.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校的学生为了对小雁塔有基本的认识,在老师的带领下对小雁塔进行了测量.测量方法如下:如图,间接测得小雁塔地部点D到地面上一点E的距离为115.2米,小雁塔的顶端为点B,且BD⊥DE,在点E处竖直放一个木棒,其顶端为C,CE=1.72米,在DE的延长线上找一点A,使A、C、B三点在同一直线上,测得AE=4.8米.求小雁塔的高度.

-
科目: 来源: 题型:
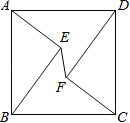
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )
A.
 B.
B. 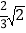 C.
C. 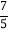 D.
D. 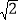
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有_______________(请填写所有正确结论的序号)
①在一个装有2白球和3个红球的袋中摸3个球,摸到红球是必然事件.②若
 ,则
,则 ; ③已知反比例函数
; ③已知反比例函数 ,若
,若 ,则
,则 ; ④分式
; ④分式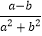 是最简分式 ; ⑤
是最简分式 ; ⑤ 和
和 是同类二次根式;
是同类二次根式; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
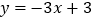 与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线
与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线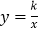 (
(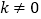 )上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线
)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线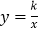 (
(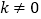 )上的点D1处,则a= .
)上的点D1处,则a= .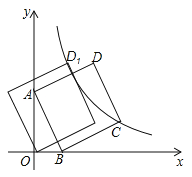
-
科目: 来源: 题型:
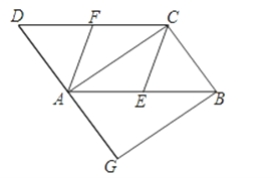
查看答案和解析>>【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
相关试题

