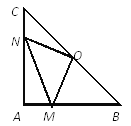
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
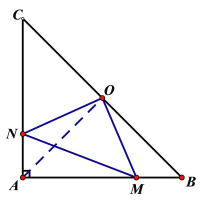
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
参考答案:
【答案】(1)OA=OB=OC. (2)△OMN为等腰直角三角形.
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半,直接得出OA=OB=OC;
(2)连接OA,证△ANO≌△BMO,即可得出ON=OM,∠MON=90°,从而△OMN是等腰直角三角形.
(1)![]() .
.
(2)![]() .
.
证明:![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()

![]() ≌
≌![]() .
.
![]() ,
, ![]() ,
,
![]() .
.
![]() .
.
故答案为:(1)OA=OC=OB (2)OMN为等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数图象的顶点在原点O,经过点A(1,
 );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.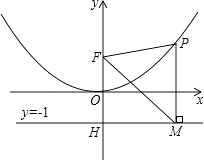
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,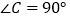 ,
, ,
, ,现将直角边
,现将直角边 沿直线
沿直线 折叠,使它落在斜边
折叠,使它落在斜边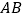 上,且与
上,且与 重合,求
重合,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2﹣3xy+4=0,③x2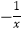 =4,④x2=0,⑤x2﹣3x﹣4=0.
=4,④x2=0,⑤x2﹣3x﹣4=0.
A.①②
B.①②④⑤
C.①③④
D.①④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A.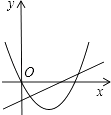
B.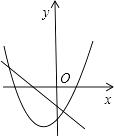
C.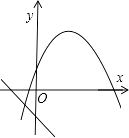
D.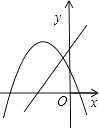
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
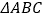 和
和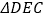 都是等腰直角三角形,
都是等腰直角三角形,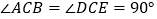 ,
,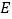 在线段
在线段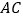 上,连接
上,连接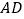 ,
, 的延长线交
的延长线交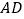 于
于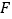 .
.(1)猜想线段
 、
、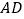 的关系;(不必证明)
的关系;(不必证明)(2)当点
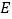 为
为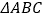 内部一点时,使点
内部一点时,使点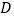 和点
和点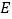 分别在
分别在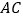 的两侧,其它条件不变.请你在图2中补全图形,则(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.
的两侧,其它条件不变.请你在图2中补全图形,则(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.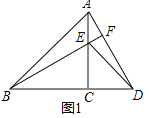
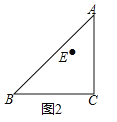
-
科目: 来源: 题型:
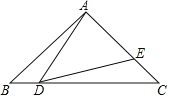
查看答案和解析>>【题目】如图,在
 中,
中,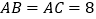 ,
,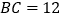 ,点
,点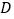 从
从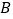 出发以每秒
出发以每秒 个单位的速度在线段
个单位的速度在线段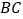 上从点
上从点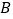 向点
向点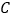 运动,点
运动,点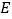 同时从
同时从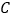 出发以每秒
出发以每秒 个单位的速度在线段
个单位的速度在线段 上向点
上向点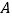 运动,连接
运动,连接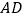 、
、 ,设
,设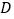 、
、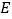 两点运动时间为
两点运动时间为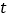 秒
秒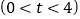 .
.
(1)运动 秒时,
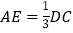 ;
;(2)运动多少秒时,
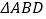 ≌
≌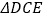 能成立;
能成立;(3)若
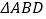 ≌
≌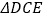 ,
, ,求
,求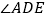 的大小.(用含
的大小.(用含 的式子表示)
的式子表示)
相关试题

