【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 出发以每秒
出发以每秒![]() 个单位的速度在线段
个单位的速度在线段![]() 上从点
上从点![]() 向点
向点![]() 运动,点
运动,点![]() 同时从
同时从![]() 出发以每秒
出发以每秒![]() 个单位的速度在线段
个单位的速度在线段![]() 上向点
上向点![]() 运动,连接
运动,连接![]() 、
、![]() ,设
,设![]() 、
、![]() 两点运动时间为
两点运动时间为![]() 秒
秒![]() .
.
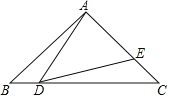
(1)运动 秒时,![]() ;
;
(2)运动多少秒时,![]() ≌
≌![]() 能成立;
能成立;
(3)若![]() ≌
≌![]() ,
,![]() ,求
,求![]() 的大小.(用含
的大小.(用含![]() 的式子表示)
的式子表示)
参考答案:
【答案】(1)3;(2)当运动2秒时;(3)∠ADE=90°﹣![]() α.
α.
【解析】
(1)由题意得BD=CE=2t,则有CD=12﹣2t,AE=8﹣2t,可得出方程8-2t=![]() (12-2t),求出方程的解即可;
(12-2t),求出方程的解即可;
(2)若ΔABD≌ΔDCE,根据全等三角形的性质则有DC=AB=8,从而可得BD=4,继而求得时间;
(3)当△ABD≌△DCE时,有∠CDE=∠BAD,继而可求得∠ADE=∠B,结合等腰三角形的性质即可得∠ADE=90°﹣![]() α.
α.
(1)由题可得,BD=CE=2t,
∴CD=12﹣2t,AE=8﹣2t,
∴当AE=![]() DC,时,8﹣2t=
DC,时,8﹣2t=![]() (12﹣2t),
(12﹣2t),
解得t=3,
故答案为:3;
(2)∵AB=AC,
∴∠B=∠C,
若ΔABD≌ΔDCE,则有DC=AB=8,
∴BD=BC-CD=12-8=4,
此时t=2,CE=2t=4,
所以当运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,
∴∠ADE=∠B.
又∵∠BAC=α,AB=AC,
∴∠ADE=∠B=![]() 180°﹣α)=90°﹣
180°﹣α)=90°﹣![]() α.
α.
-
科目: 来源: 题型:
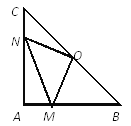
查看答案和解析>>【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A.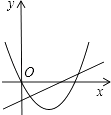
B.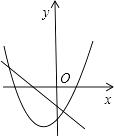
C.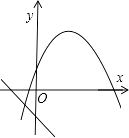
D.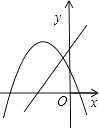
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
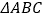 和
和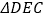 都是等腰直角三角形,
都是等腰直角三角形,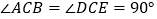 ,
,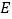 在线段
在线段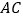 上,连接
上,连接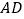 ,
, 的延长线交
的延长线交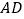 于
于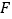 .
.(1)猜想线段
 、
、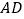 的关系;(不必证明)
的关系;(不必证明)(2)当点
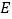 为
为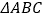 内部一点时,使点
内部一点时,使点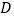 和点
和点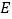 分别在
分别在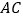 的两侧,其它条件不变.请你在图2中补全图形,则(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.
的两侧,其它条件不变.请你在图2中补全图形,则(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.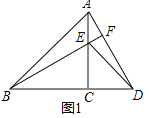
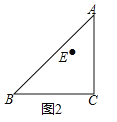
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,在
 的边
的边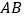 上取一点
上取一点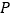 ,连接
,连接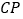 ,可以把
,可以把 分成两个三角形,如果这两个三角形都是等腰三角形,我们就称点
分成两个三角形,如果这两个三角形都是等腰三角形,我们就称点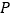 是
是 的边
的边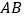 上的和谐点.
上的和谐点.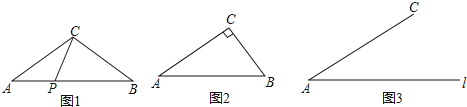
(1)如图2,在
 中,
中,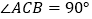 ,试找出边
,试找出边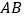 上的和谐点
上的和谐点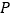 ;
;(2)如图3,已知
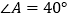 ,
, 的顶点
的顶点 在射线
在射线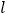 上,点
上,点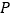 是边
是边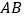 上的和谐点,请在图3中画出所有符合条件的
上的和谐点,请在图3中画出所有符合条件的 点,并写出相应的
点,并写出相应的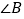 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学研究课上,老师出示如图1所示的长方形纸条
 ,
, ,
, ,然后在纸条上任意画一条截线段
,然后在纸条上任意画一条截线段 ,将纸片沿
,将纸片沿 折叠,
折叠,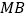 与
与 交于点
交于点 ,得到
,得到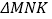 ,如图2所示:
,如图2所示:
(1)若
 ,求
,求 的大小;
的大小;(2)改变折痕
 位置,判断
位置,判断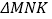 的形状,并说明理由;
的形状,并说明理由;(3)爱动脑筋的小明在研究
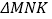 的面积时,发现
的面积时,发现 边上的高始终是个不变的值.根据这一发现,他很快研究出
边上的高始终是个不变的值.根据这一发现,他很快研究出 的面积最小值为
的面积最小值为 ,求
,求 的大小;
的大小;(4)小明继续动手操作,发现了
 面积的最大值,请你求出这个最大值.
面积的最大值,请你求出这个最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A.k>
B.k≥
C.k> 且k≠1
且k≠1
D.k≥ 且k≠1
且k≠1
相关试题

