【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:

(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?
(2)已知洗衣机的排水速度为每分钟19升.
①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
参考答案:
【答案】(1)洗衣机的进水时间是4分钟;清洗时洗衣机中水量为40升.(2)排水时间为2分钟,排水结束时洗衣机中剩下的水量为2升.
【解析】
解:(1)依题意得洗衣机的进水时间是4分钟,清洗时洗衣机中的水量是40升;
(2)①∵洗衣机的排水速度为每分钟19升,从第15分钟开始排水,排水量为40升,
∴y=40-19(x-15)=-19x+325,
②∵排水时间为2分钟,
∴y=-19×(15+2)+325=2升.
∴排水结束时洗衣机中剩下的水量2升.
(1)根据函数图象可以确定洗衣机的进水时间,清洗时洗衣机中的水量;
(2)①由于洗衣机的排水速度为每分钟19升,并且从第15分钟开始排水,排水量为40升,由此即可确定排水时y与x之间的关系式;
②根据①中的结论代入已知数值即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 圆柱形容器中,高为
 底面周长为
底面周长为 在容器内壁离容器底部
在容器内壁离容器底部 的点
的点 处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿
处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿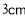 与蚊子相对的点
与蚊子相对的点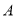 处,则壁虎捕捉蚊子的最短距离为___
处,则壁虎捕捉蚊子的最短距离为___ (容器厚度忽略不计. )
(容器厚度忽略不计. )
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
 中,动点
中,动点 分别从
分别从 两点同时出发,以相同的速度在直线
两点同时出发,以相同的速度在直线 上移动;
上移动;(1)如图①,当
 分别移动到边
分别移动到边 的延长线上时,连接
的延长线上时,连接 和
和 与
与 的关系为____ ;
的关系为____ ;
(2)如图②,己知正方形的边长为
 点
点 和
和 分别从点
分别从点 同时出发,以相同的速度沿
同时出发,以相同的速度沿 方向向终点
方向向终点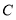 和
和 运动,连接
运动,连接 和
和 ,交于点
,交于点 ,请你画出点
,请你画出点 运动路线的草图,试求出线段
运动路线的草图,试求出线段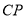 的最小值.
的最小值.
(3)如图③,在(2)的条件下,求
 周长的最大值;
周长的最大值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
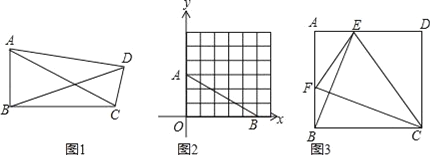
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在
 中,已知
中,已知 分别是
分别是 上的两点,且
上的两点,且 .
. .
. 求梯形
求梯形 的面积;
的面积; 如图②,有一梯形
如图②,有一梯形 与梯形
与梯形 重合,固定
重合,固定 ,将梯形
,将梯形 向右运动,当点D与点C重合时梯形
向右运动,当点D与点C重合时梯形 停止运动;
停止运动;
①若某时段运动后形成的四边形
 中,
中, 求运动路程
求运动路程 的长,并求此时
的长,并求此时 的值;
的值;②设运动中
 的长度为
的长度为 ,试用含
,试用含 的代数式表示梯形
的代数式表示梯形 与
与 重合部分面积
重合部分面积 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 的两条高
的两条高 交于点
交于点 ,点
,点 分别是
分别是 ,
, 的中点,连接
的中点,连接 .
.
 求证:
求证: 垂直平分
垂直平分 ;
; 若
若 .判断以
.判断以 为顶点的四边形的形状,并证明你的结论.
为顶点的四边形的形状,并证明你的结论.
相关试题

