【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
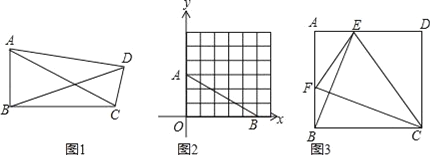
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
参考答案:
【答案】(1)![]() (2)(5,3),(3,5)(3)
(2)(5,3),(3,5)(3)![]() ;
;![]() ;
;![]()
【解析】试题分析:(1)利用准矩形的定义和勾股定理计算,再根据准矩形的特点和整点的特点求出即可;
(2)先利用正方形的性质判断出△ABE≌△BCF,即可;
(2)分三种情况分别计算,用到梯形面积公式,对角线面积公式,对角线互相垂直的四边形的面积计算方法.
试题解析:(1)①∵∠ABC=90,
∴BD=![]() ,
,
故答案为![]() ,
,
②∵A(0,3),B(5,0),
∴AB=![]() =6,
=6,
设点P(m,n),A(0,0),
∴OP=![]() =6,
=6,
∵m,n都为整数,
∴点P(3,5)或(5,3);
故答案为P(3,5)或(5,3);
(2)∵四边形ABCD是正方形,
∴AB=BC∠A=∠ABC=90°,
∴∠EAF+∠EBC=90°,
∵BE⊥CF,
∴∠EBC+∠BCF=90°,
∴∠EBF=∠BCF,
∴△ABE≌△BCF,
∴BE=CF,
∴四边形BCEF是准矩形;
(3)![]() ;
;![]() ;
;![]()
∵∠ABC=90°,∠BAC=60°,AB=2,
∴BC=2![]() ,AC=4,
,AC=4,
准矩形ABCD中,BD=AC=4,
①当AC=AD时,如图1,作DE⊥AB,
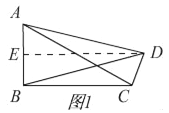
∴AE=BE![]() AB=1,
AB=1,
∴DE=![]() ,
,
∴S准矩形ABCD=S△ADE+S梯形BCDE
=![]() DE×AE+
DE×AE+![]() (BC+DE)×BE
(BC+DE)×BE
=![]() ×
×![]() +
+![]() (2
(2![]() +
+![]() )×1
)×1
=![]() +
+![]() ;
;
②当AC=CD时,如图2,

作DF⊥BC,
∴BD=CD,
∴BF=CF=![]() BC=
BC=![]() ,
,
∴DF=![]() ,
,
∴S准矩形ABCD=S△DCF+S梯形ABFD
=![]() FC×DF+
FC×DF+![]() (AB+DF)×BF
(AB+DF)×BF
=![]() ×
×![]() ×
×![]() +
+![]() (2+
(2+![]() )×
)×![]()
=![]() +
+![]() ;
;
③当AD=CD,如图3,
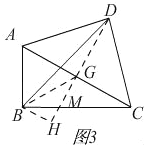
连接AC中点和D并延长,连接BG,过B作BH⊥DG,
∴BD=CD=AC=4,
∴AG=![]() AC=2,
AC=2,
∵AB=2,
∴AB=AG,
∵∠BAC=60°,
∴∠ABG=60°,
∴∠CBG=30°
在Rt△BHG中,BG=2,∠BGH=30°,
∴BH=1,
在Rt△BHM中,BH=1,∠CBH=30°,
∴BM=![]() ,HM=
,HM=![]() ,
,
∴CM=![]() ,
,
在Rt△DHB中,BH=1,BD=4,
∴DH=![]() ,∴DM=DH﹣MH=
,∴DM=DH﹣MH=![]() ﹣
﹣![]() ,
,
∴S准矩形ABCD=S△DCF+S四边形AMCD
=![]() BM×AB+
BM×AB+![]() AC×DM
AC×DM
=![]() ×
×![]() ×2+
×2+![]() ×4×(
×4×(![]() ﹣
﹣![]() )
)
=2![]() ;
;
故答案为![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时)
…
5
10
20
32
40
48
…
流量q(辆/小时)
…
550
1000
1600
1792
1600
1152
…
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ②
②  ③
③ 
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足 ,请结合(1)中选取的函数关系式继续解决下列问题:
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当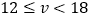 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 圆柱形容器中,高为
 底面周长为
底面周长为 在容器内壁离容器底部
在容器内壁离容器底部 的点
的点 处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿
处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿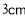 与蚊子相对的点
与蚊子相对的点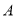 处,则壁虎捕捉蚊子的最短距离为___
处,则壁虎捕捉蚊子的最短距离为___ (容器厚度忽略不计. )
(容器厚度忽略不计. )
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
 中,动点
中,动点 分别从
分别从 两点同时出发,以相同的速度在直线
两点同时出发,以相同的速度在直线 上移动;
上移动;(1)如图①,当
 分别移动到边
分别移动到边 的延长线上时,连接
的延长线上时,连接 和
和 与
与 的关系为____ ;
的关系为____ ;
(2)如图②,己知正方形的边长为
 点
点 和
和 分别从点
分别从点 同时出发,以相同的速度沿
同时出发,以相同的速度沿 方向向终点
方向向终点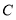 和
和 运动,连接
运动,连接 和
和 ,交于点
,交于点 ,请你画出点
,请你画出点 运动路线的草图,试求出线段
运动路线的草图,试求出线段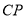 的最小值.
的最小值.
(3)如图③,在(2)的条件下,求
 周长的最大值;
周长的最大值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:

(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?
(2)已知洗衣机的排水速度为每分钟19升.
①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在
 中,已知
中,已知 分别是
分别是 上的两点,且
上的两点,且 .
. .
. 求梯形
求梯形 的面积;
的面积; 如图②,有一梯形
如图②,有一梯形 与梯形
与梯形 重合,固定
重合,固定 ,将梯形
,将梯形 向右运动,当点D与点C重合时梯形
向右运动,当点D与点C重合时梯形 停止运动;
停止运动;
①若某时段运动后形成的四边形
 中,
中, 求运动路程
求运动路程 的长,并求此时
的长,并求此时 的值;
的值;②设运动中
 的长度为
的长度为 ,试用含
,试用含 的代数式表示梯形
的代数式表示梯形 与
与 重合部分面积
重合部分面积 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
相关试题

