【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
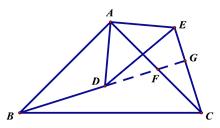
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.

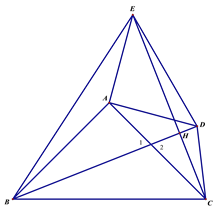
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.
①若BD=![]() ,求四边形BCDE的面积;
,求四边形BCDE的面积;
②若AB=3,AD=2,设CD2=x,EB2=y,求y与x之间的函数关系式.

参考答案:
【答案】(1)BD=CE,BD⊥CE;
(2)BD⊥CE,理由见解析;
(3)①S四边形BCDE=![]() ;②y=26-x
;②y=26-x
【解析】试题分析:(1)由等腰直角三角形的性质即可得出;
(2)由边角边证得△ABD≌△ACE,由全等三角形的性质得出∠ABD=∠ACE,延长BD,由三角形内角和即可得∠CGF=∠BAF=90°,即可证得垂直;
(3)①易证△ABD≌△ACE,可得∠BHC=∠BAC=90°,即BD⊥CE,即可求得四边形BCDE的面积;
②由勾股定理等量代换即可求得y与x之间的函数关系式.
试题解析:(1)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC.AD=AE,
∴AB-AD=AC-AE,即:BD=CE,
∵BD、CE相交于点A,∠BAC=90°,
∴BD⊥CE;
(2)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC-∠DAC, ∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE,
延长BD,分别交AC,CE于F,G,BD=CE,
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AFB=∠GFC,
∴∠CGF=∠BAF=90°,即BD⊥CE;
(3)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE,∠ABD=∠ACE
∵∠1=∠2
∴∠BHC=∠BAC=90°
∴S四边形BCDE=S△BCE+S△DCE= ![]() =
= ![]() =
=![]() ,
,
∵∠BHC=90°,
∴CD2+EB2=CH2+HD2+EH2+HB2=CH2+HB2+EH2+HD2=BC2+DE2=(![]() )2+(
)2+(![]() )2=26,
)2=26,
∴y=26-x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2009年起,每年的11月11日是Tmall一年一度全场大促销的日子.某服饰店对某商品推出促销活动:双十一当天,买两件等值的商品可在每件原价减50元的基础上,再打八折;如果单买,则按原价购买.
(1)妮妮看中两件原价都是300元的此类商品, 则在双十一当天,购买这两件商品总共需要多少钱?
(2)熊熊购买了两件等值的此类商品后, 发现比两件一起按原价六折购买便宜. 若这两件等值商品的价格都是大于196的整数, 则原价可能是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年下半年猪肉价格一路上涨,为平抑猪肉价格,商务部会同国家发展委员会、财政部自9月19日以来累计向市场投放中央储备猪肉31000吨,请将31000用科学记数法表示为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( ).
A.两个负数,绝对值大的反而小
B.数轴上右边的点表示的数总是比左边的点表示的数大
C.等式两边除以同一个数等式仍然成立
D.一元一次不等式组的解集是不等式组中各不等式解集的公共部分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
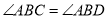 ,要使
,要使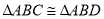 ,还需添加一个条件,那么在①
,还需添加一个条件,那么在①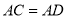 ;②
;②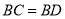 ;③
;③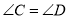 ;④
;④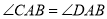 这四个关系中可以选择的是
这四个关系中可以选择的是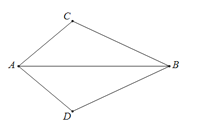
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算 (﹣1)2×(﹣23)﹣(﹣4)÷2×

(2)先化简,再求值已知2(3a2b﹣5ab2)﹣3(2a2b﹣3ab2),其中a=﹣1,b=3.
(3)解方程:3(x﹣3)+1=x﹣(2x﹣1)
(4)解方程:
 ﹣
﹣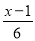 =2
=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径长为R=5,弦AB 与弦CD平行,他们之间距离为7,AB=6求:弦CD的长.

相关试题

