【题目】把所有正偶数从小到大排列,并按如下规律分组:(2)、(4,6),(8,10,12),(14,16,18,20),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左往右数).如A2=(1,1),A10=(3,2),A18=(4,3),则A200可表示为( )
A.(14,9)B.(14,10)C.(15,9)D.(15,10)
参考答案:
【答案】A
【解析】
根据数字的变化可知200是第100个数,然后判断第100个数在第几组,进一步判断这个数是第几个数即可.
解:200是第100个数,
设200在第n组,则
1+2+3+…+n=![]() n(n+1)
n(n+1)
当n=13时,![]() n(n+1)=91,
n(n+1)=91,
当n=14时,![]() n(n+1)=105,
n(n+1)=105,
∴第100个数在第14组,
第14组的第一个数是2×91+2=184,
则200是第(![]() +1)=9个数,
+1)=9个数,
∴A200=(14,9).
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
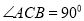 , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则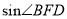 的值为_____________.
的值为_____________.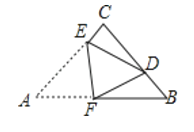
【答案】
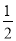
【解析】分析:过点D作DG
 AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,在Rt△DCE中,由勾股定理求得
 ,所以DB=
,所以DB=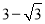 ;在Rt△ABC中,由勾股定理得
;在Rt△ABC中,由勾股定理得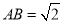 ;在Rt△DGB中,由锐角三角函数求得
;在Rt△DGB中,由锐角三角函数求得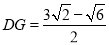 ,
, 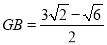 ;
;设AF=DF=x,则FG=
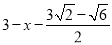 ,在Rt△DFG中,根据勾股定理得方程
,在Rt△DFG中,根据勾股定理得方程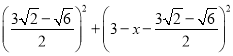 =
=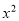 ,解得
,解得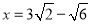 ,从而求得
,从而求得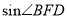 .的值
.的值详解:
如图所示,过点D作DG
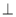 AB于点G.
AB于点G.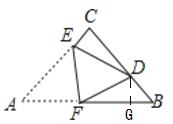
根据折叠性质,可知△AEF
 △DEF,
△DEF,∴AE=DE=2,AF=DF,CE=AC-AE=1,
在Rt△DCE中,由勾股定理得
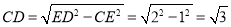 ,
,∴DB=
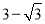 ;
;在Rt△ABC中,由勾股定理得
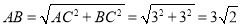 ;
;在Rt△DGB中,
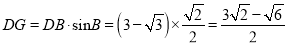 ,
, 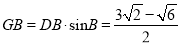 ;
;设AF=DF=x,得FG=AB-AF-GB=
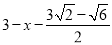 ,
,在Rt△DFG中,
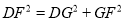 ,
,即
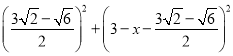 =
=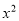 ,
,解得
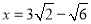 ,
,∴
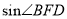 =
=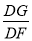 =
=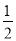 .
.故答案为:
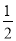 .
.点睛:主要考查了翻折变换的性质、勾股定理、锐角三件函数的定义;解题的关键是灵活运用折叠的性质、勾股定理、锐角三角函数的定义等知识来解决问题.
【题型】填空题
【结束】
18【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】首先,我们学习一道“最值”问题的解答:
问题:已知x>0,求
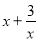 的最小值.
的最小值.解答:对于x>0,我们有:
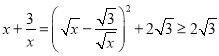
当
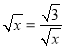 ,即
,即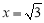 时,上述不等式取等号,所以
时,上述不等式取等号,所以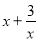 的最小值是
的最小值是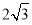
由解答知,
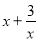 的最小值是
的最小值是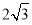 .
.弄清上述问题及解答方法之后,解答下述问题:
(1)求
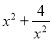 的最小值.
的最小值.(2)在直角坐标系 xOy 中,一次函数
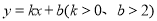 的图象与 x 轴、 y 轴分别交于 A 、 B 两点.
的图象与 x 轴、 y 轴分别交于 A 、 B 两点.①求 A 、 B 两点的坐标;
②求当OAB 的面积值等于
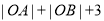 时,用b 表示 k ;
时,用b 表示 k ;③在②的条件下,求AOB 面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在八年级举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查30名学生的听写汉字的正确字数如下:
2
9
17
24
33
5
12
19
26
34
7
14
20
26
36
15
22
26
39
31
22
27
39
22
28
23
23
31
30
28
对这30个数据按组距8进行分组,并统计整理.
(1)请完成下面频数分布统计表;
组别
正确字数x
频数
A
0≤x<8
B
8≤x<16
C
16≤x<24
D
24≤x<32
E
32≤x<40
(2)在上图中请画出频数分布直方图;
(3)若该校八年级学生共有1200人,如果听写正确的个数少于24个定为不合格,请你估计该校八年级本次比赛听写不合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简与求值
(1)求3x2+x+3(x2﹣
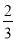 x)﹣(6x2+x)的值,其中x=﹣6.
x)﹣(6x2+x)的值,其中x=﹣6.(2)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣
 )2=0
)2=0 -
科目: 来源: 题型:
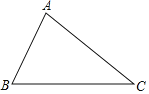
查看答案和解析>>【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
-
科目: 来源: 题型:
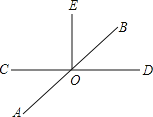
查看答案和解析>>【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
相关试题

