【题目】等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?

参考答案:
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]()
【解析】分析:(1)分析易得,第一次相切时,与斜边相切,假设此时,△ABC移至△A′B′C′处,A′C′与⊙O切于点E,连OE并延长,交B′C′于F.由切线长定理易得CC′的长,进而由三角形运动的速度可得答案;
(2)设运动的时间为t秒,根据题意得:CC′=2t,DD′=t,则C′D′=CD+DD′-CC′=4+t-2t=4-t,由第(1)的结论列式得出结果;
(3)求出相切的时间,进而得出B点移动的距离.
详解:(1)假设第一次相切时,△ABC移至△A′B′C′处,
如图1,A′C′与⊙O切于点E,连接OE并延长,交B′C′于F,
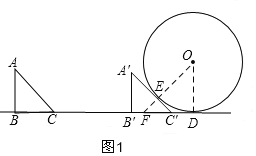
设⊙O与直线l切于点D,连接OD,则OE⊥A′C′,OD⊥直线l,
由切线长定理可知C′E=C′D,
设C′D=x,则C′E=x,
∵△ABC是等腰直角三角形,
∴∠A=∠ACB=45°,
∴∠A′C′B′=∠ACB=45°,
∴△EFC′是等腰直角三角形,
∴C′F=![]() x,∠OFD=45°,
x,∠OFD=45°,
∴△OFD也是等腰直角三角形,
∴OD=DF,
∴![]() x+x=1,则x=
x+x=1,则x=![]() -1,
-1,
∴CC′=BD-BC-C′D=5-1-(![]() -1)=5-
-1)=5-![]() ,
,
∴点C运动的时间为![]() ;
;
则经过![]() 秒,△ABC的边与圆第一次相切;
秒,△ABC的边与圆第一次相切;
(2)如图2,设经过t秒△ABC的边与圆第一次相切,△ABC移至△A′B′C′处,⊙O与BC所在直线的切点D移至D′处,
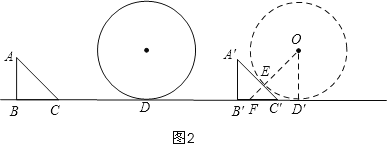
A′C′与⊙O切于点E,连OE并延长,交B′C′于F,
∵CC′=2t,DD′=t,
∴C′D′=CD+DD′-CC′=4+t-2t=4-t,
由切线长定理得C′E=C′D′=4-t,
由(1)得:4-t=![]() -1,
-1,
解得:t=5-![]() ,
,
答:经过5-![]() 秒△ABC的边与圆第一次相切;
秒△ABC的边与圆第一次相切;
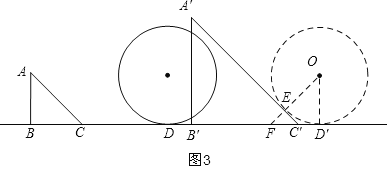
(3)由(2)得CC′=(2+0.5)t=2.5t,DD′=t,
则C′D′=CD+DD′-CC′=4+t-2.5t=4-1.5t,
由切线长定理得C′E=C′D′=4-1.5t,
由(1)得:4-1.5t=![]() -1,
-1,
解得:t=![]() ,
,
∴点B运动的距离为2×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=
 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>

 的x的取值范围;
的x的取值范围;(3)若点P在x轴上,且S△ACP=
 S△BOC,求点P的坐标.
S△BOC,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校以随机抽样的方式开展了“中学生喜欢数学的程度”的问卷调查,调查的结果分为A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级,图1、图2是根据采集的数据绘制的两幅不完整的统计图.
请根据统计图提供的信息,回答下列问题:
(1)C等级所占的圆心角为________°;
(2)请直接在图2中补全条形统计图;
(3)若该校有学生1000人,请根据调查结果,估计“比较喜欢”的学生人数为多少人.
某校“中学生喜欢数学的程度”的扇形统计图 某校“中学生喜欢数学的程度”的条形统计图

-
科目: 来源: 题型:
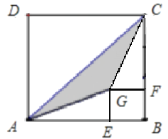
查看答案和解析>>【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
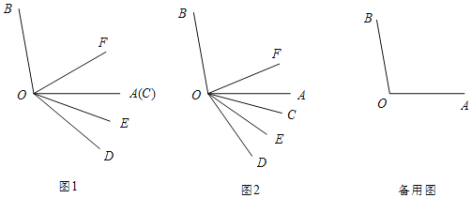
查看答案和解析>>【题目】已知∠AOB=100°,∠COD=40°,OE,OF分别平分∠AOD,∠BOD.
(1)如图1,当OA,OC重合时,求∠EOF的度数;
(2)若将∠COD的从图1的位置绕点O顺时针旋转,旋转角∠AOC=α,且0°<α<90°.
①如图2,试判断∠BOF与∠COE之间满足的数量关系并说明理由.
②在∠COD旋转过程中,请直接写出∠BOE,∠COF,∠AOC之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠BDC=30°,DC=4,AE⊥BD于E,CF⊥BD于F,且E、F恰好是BD的三等分点,AE、CF的延长线分别交DC、AB于N、M点,那么四边形MENF的面积是( )

A.
 B.
B. C.2
C.2 D.2
D.2
相关试题

