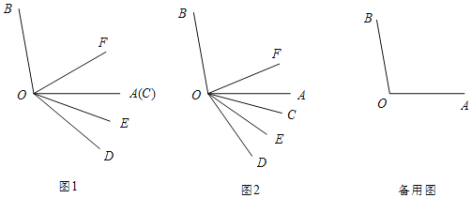
【题目】已知∠AOB=100°,∠COD=40°,OE,OF分别平分∠AOD,∠BOD.
(1)如图1,当OA,OC重合时,求∠EOF的度数;
(2)若将∠COD的从图1的位置绕点O顺时针旋转,旋转角∠AOC=α,且0°<α<90°.
①如图2,试判断∠BOF与∠COE之间满足的数量关系并说明理由.
②在∠COD旋转过程中,请直接写出∠BOE,∠COF,∠AOC之间的数量关系.
参考答案:
【答案】(1)∠EOF=50°;(2)①∠BOF+∠COE=90°;理由见解析;②∠COF+∠AOC﹣∠BOE=30°.
【解析】
(1)由题意得出∠AOD=∠COD=40°,∠BOD=∠AOB+∠COD=140°,由角平分线定义得出∠EOD=![]() ∠AOD=20°,∠DOF=
∠AOD=20°,∠DOF=![]() ∠BOD=70°,即可得出答案;
∠BOD=70°,即可得出答案;
(2)①由角平分线定义得出∠EOD=∠AOE=![]() ∠AOD=20°+
∠AOD=20°+![]() α,∠BOF=
α,∠BOF=![]() ∠BOD=70°+
∠BOD=70°+![]() α,求出∠COE=∠AOE﹣∠AOC=20°﹣
α,求出∠COE=∠AOE﹣∠AOC=20°﹣![]() α,即可得出答案;
α,即可得出答案;
②由①得∠EOD=∠AOE=20°+![]() α,∠DOF=∠BOF=70°+
α,∠DOF=∠BOF=70°+![]() α,
α,
当∠AOC<40°时,求出∠COF=∠DOF﹣∠COD=30°+![]() α,∠BOE=∠BOD﹣∠EOD=∠AOB+∠COD+α﹣∠EOD=120°+
α,∠BOE=∠BOD﹣∠EOD=∠AOB+∠COD+α﹣∠EOD=120°+![]() α,即可得出答案;
α,即可得出答案;
当40°<∠AOC<90°时,求出∠COF=∠DOF+∠DOC=150°﹣![]() α,∠BOE=∠BOD﹣∠DOE=120°+
α,∠BOE=∠BOD﹣∠DOE=120°+![]() ,即可得出答案.
,即可得出答案.
解:(1)∵OA,OC重合,
∴∠AOD=∠COD=40°,∠BOD=∠AOB+∠COD=100°+40°=140°,
∵OE平分∠AOD,OF平分∠BOD,
∴∠EOD=![]() ∠AOD=
∠AOD=![]() ×40°=20°,∠DOF=
×40°=20°,∠DOF=![]() ∠BOD=
∠BOD=![]() ×140°=70°,
×140°=70°,
∴∠EOF=∠DOF﹣∠EOD=70°﹣20°=50°;
(2)①∠BOF+∠COE=90°;理由如下:
∵OE平分∠AOD,OF平分∠BOD,
∴∠EOD=∠AOE=![]() ∠AOD=
∠AOD=![]() (40°+α)=20°+
(40°+α)=20°+![]() α,∠BOF=
α,∠BOF=![]() ∠BOD=
∠BOD=![]() (∠AOB+∠COD+α)=
(∠AOB+∠COD+α)=![]() (100°+40°+α)=70°+
(100°+40°+α)=70°+![]() α,
α,
∴∠COE=∠AOE﹣∠AOC=20°+![]() α﹣α=20°﹣
α﹣α=20°﹣![]() α,
α,
∴∠BOF+∠COE=70°+![]() α+20°﹣
α+20°﹣![]() α=90°;
α=90°;
②由①得:∠EOD=∠AOE=20°+![]() α,∠DOF=∠BOF=70°+
α,∠DOF=∠BOF=70°+![]() α,
α,
当∠AOC<40°时,如图2所示:
∠COF=∠DOF﹣∠COD=70°+![]() α﹣40°=30°+
α﹣40°=30°+![]() α,
α,
∠BOE=∠BOD﹣∠EOD=∠AOB+∠COD+α﹣∠EOD=100°+40°+α﹣(20°+![]() α)=120°+
α)=120°+![]() α,
α,
∴∠BOE+∠COF﹣∠AOC=120°+![]() α+30°+
α+30°+![]() α﹣α=150°,
α﹣α=150°,
当40°<∠AOC<90°时,如图3所示:
∠COF=∠DOF+∠DOC=![]() (360°﹣140°﹣α)+40°=150°﹣
(360°﹣140°﹣α)+40°=150°﹣![]() α,
α,
∠BOE=∠BOD﹣∠DOE=140°+α﹣(20°+![]() α)=120°+
α)=120°+![]() ,
,
∴∠COF+∠AOC﹣∠BOE=150°﹣![]() +α﹣(120°+
+α﹣(120°+![]() )=30°;
)=30°;
综上所述,∠BOE,∠COF,∠AOC之间的数量关系为∠BOE+∠COF﹣∠AOC=150°或∠COF+∠AOC﹣∠BOE=30°.


-
科目: 来源: 题型:
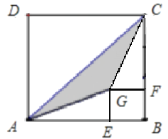
查看答案和解析>>【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠BDC=30°,DC=4,AE⊥BD于E,CF⊥BD于F,且E、F恰好是BD的三等分点,AE、CF的延长线分别交DC、AB于N、M点,那么四边形MENF的面积是( )

A.
 B.
B. C.2
C.2 D.2
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分7分)已知关于x的方程
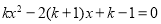 有两个不相等的实数根.
有两个不相等的实数根.(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使得△MNP为等腰直角三角形,则符合条件的点P有(提示:直角三角形斜边上的中线等于斜边的一半)( )

A. 2个 B. 3个 C. 4个 D. 5个
相关试题

