【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
参考答案:
【答案】C
【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.
解:作DA延长线A A″,

∵∠DAB=130°,
∴∠HAA′=50°,
∴∠AA′M+∠A″=∠HAA′=50°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×50°=100°,
故选C.
“点睛”本题考查的是轴对称-最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M、N的位置是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)(a2)3÷(-a)2;(2)(a+2b)(a+b)-3a(a+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣4,2,﹣1,3这四个数中,比﹣2小的数是( )
A.-4
B.2
C.-1
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,在△ABC中,点Q,P分别是边AC,BC上的点,AQ=PQ,PR⊥AB于R,PS⊥AC于S,且PR=PS,下面四个结论:①AP平分∠BAC;②AS=AR;③BP=QP;④QP∥AB.其中一定正确的是( )
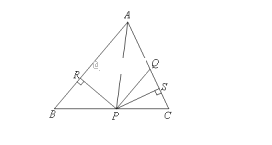
A. ①②③ B. ①③④ C. ①②④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 和一次函数
和一次函数 .
.(1)当t=0时,试判断二次函数
 的图象与x轴是否有公共点,如果有,请写出公共点的坐标;
的图象与x轴是否有公共点,如果有,请写出公共点的坐标;(2)若二次函数
 的图象与x轴的两个不同公共点,且这两个公共点间的距离为8,求t的值;
的图象与x轴的两个不同公共点,且这两个公共点间的距离为8,求t的值;(3)求证:不论实数t取何值,总存在实数x,使
 ≥
≥ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】按一定规律排列的一列数:21 , 22 , 23 , 25 , 28 , 213 , …,若x、y、z表示这列数中的连续三个数,猜想x、y、z满足的关系式是 .
-
科目: 来源: 题型:
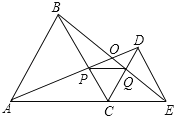
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
相关试题

