Question

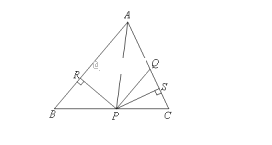
【题目】如右图，在△ABC中，点Q，P分别是边AC，BC上的点，AQ=PQ，PR⊥AB于R，PS⊥AC于S，且PR=PS，下面四个结论：①AP平分∠BAC；②AS=AR；③BP=QP；④QP∥AB．其中一定正确的是( )

A. ①②③ B. ①③④ C. ①②④ D. ②③④

Answer 1

【答案】C

【解析】试题解析：∵PR⊥AB于点R，PS⊥AC于点S，且PR=PS，

∴点P在∠BAC的平分线上，

即AP平分∠BAC，故①正确；

∴∠PAR=∠PAQ，

∵AQ=PQ，

∴∠APQ=∠PAQ，

∴∠APQ=∠PAR，

故④正确；

在△APR与△APS中,

∴AR=AS，故②正确；

△BPR和△QSP只能知道PR=PS,∠BRP=∠QSP=90，其他条件不容易得到，所以，不一定全等.故③错误.

故选C.