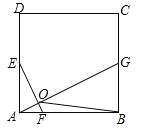
【题目】如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=![]() AB.
AB.
(1)求证:EF⊥AG;
(2)若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当![]() ,求△PAB周长的最小值.
,求△PAB周长的最小值.
参考答案:
【答案】(1)证明见解析;(2)成立;(3)![]() .
.
【解析】
试题分析:(1)由正方形的性质得出AD=AB,∠EAF=∠ABG=90°,证出![]() ,得出△AEF∽△BAG,由相似三角形的性质得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理证出∠AOE=90°即可;
,得出△AEF∽△BAG,由相似三角形的性质得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理证出∠AOE=90°即可;
(2)证明△AEF∽△BAG,得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理即可得出结论;
(3)过O作MN∥AB,交AD于M,BC于N,则MN⊥AD,MN=AB=4,由三角形面积关系得出点P在线段MN上,当P为MN的中点时,△PAB的周长最小,此时PA=PB,PM=![]() MN=2,连接EG,则EG∥AB,EG=AB=4,证明△AOF∽△GOE,得出
MN=2,连接EG,则EG∥AB,EG=AB=4,证明△AOF∽△GOE,得出![]() =
=![]() ,证出
,证出![]() =
=![]() ,得出AM=
,得出AM=![]() AE=
AE=![]() ,由勾股定理求出PA,即可得出答案.
,由勾股定理求出PA,即可得出答案.
试题解析:(1)证明:∵四边形ABCD是正方形,∴AD=AB,∠EAF=∠ABG=90°,∵点E、G分别是边AD、BC的中点,AF=![]() AB,∴
AB,∴![]() =
=![]() ,
,![]() =
=![]() ,∴
,∴![]() ,∴△AEF∽△BAG,∴∠AEF=∠BAG,∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠AOE=90°,∴EF⊥AG;
,∴△AEF∽△BAG,∴∠AEF=∠BAG,∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠AOE=90°,∴EF⊥AG;
(2)解:成立;理由如下:
根据题意得:![]() =
=![]() ,∵
,∵![]() =
=![]() ,∴
,∴![]() =
=![]() ,又∵∠EAF=∠ABG,∴△AEF∽△BAG,∴∠AEF=∠BAG,∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠AOE=90°,∴EF⊥AG;
,又∵∠EAF=∠ABG,∴△AEF∽△BAG,∴∠AEF=∠BAG,∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠AOE=90°,∴EF⊥AG;
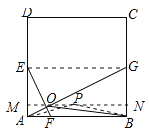
(3)解:过O作MN∥AB,交AD于M,BC于N,如图所示:
则MN⊥AD,MN=AB=4,∵P是正方形ABCD内一点,当S△PAB=S△OAB,∴点P在线段MN上,当P为MN的中点时,△PAB的周长最小,此时PA=PB,PM=![]() MN=2,连接EG、PA、PB,则EG∥AB,EG=AB=4,∴△AOF∽△GOE,∴
MN=2,连接EG、PA、PB,则EG∥AB,EG=AB=4,∴△AOF∽△GOE,∴![]() =
=![]() ,∵MN∥AB,∴
,∵MN∥AB,∴![]() =
=![]() ,∴AM=
,∴AM=![]() AE=
AE=![]() ×2=
×2=![]() ,由勾股定理得:PA=
,由勾股定理得:PA=![]() =
=![]() ,∴△PAB周长的最小值=2PA+AB=
,∴△PAB周长的最小值=2PA+AB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中结果为负数的是( )
A. (﹣5)2B. ﹣|﹣5|C. 52D. |﹣5|
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小李和小陆从 A 地出发,骑自行车沿同一条路行驶到 B 地,他们离出发地的距离s和行驶时间t之间的关系的图象如图,根据图象回答下列问题:
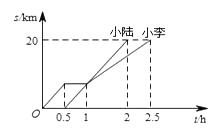
(1)小李在途中逗留的时间为h,小陆从 A 地到 B 地的速度是km/h.
(2)当小李和小陆相遇时,他们离 B 地的路程是千米;
(3)写出小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式为 -
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=x2﹣12x化为形如y=a(x﹣h)2+k的形式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线
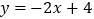 与x轴相交于点A,与y轴相交于点B.
与x轴相交于点A,与y轴相交于点B.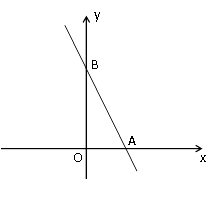
(1)直接写出A点的坐标;
(2)当x 时,y≤4;
(3)过B点作直线BP与x轴相交于P,若OP=2OA时,求ΔABP的面积。
(4)在y轴上是否存在E点,使得ΔABE为等腰三角形,若存在,直接写出满足条件的E点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知正多边形的每个外角都是45°,则从这个正多边形的一个顶点出发,共可以作_______条对角线.
相关试题

