【题目】如图,在直角坐标系中,直线 ![]() 与x轴相交于点A,与y轴相交于点B.
与x轴相交于点A,与y轴相交于点B.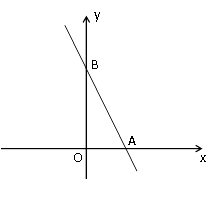
(1)直接写出A点的坐标;
(2)当x 时,y≤4;
(3)过B点作直线BP与x轴相交于P,若OP=2OA时,求ΔABP的面积。
(4)在y轴上是否存在E点,使得ΔABE为等腰三角形,若存在,直接写出满足条件的E点坐标.
参考答案:
【答案】
(1)解:A(2,0)
(2)≥ 0
(3)解:当P在A点右侧时,P(4,0)
![]()
![]()
当P在A点左侧时,P(-4,0)
![]()
![]()
![]()
(4)解: ![]()
【解析】(1)把y=0代入y = 2 x + 4中,解得x=2,所以A点的坐标为(2,0). 所以答案是A(2,0);
(2)把x=0代入y = 2 x + 4中,解得y=4,即直线 y = 2 x + 4与y轴的交点B的坐标为(4,0) ,由图象知,当x![]() 0时,y
0时,y![]() 4. 所以答案是为x
4. 所以答案是为x![]() 0;
0;
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李和小陆从 A 地出发,骑自行车沿同一条路行驶到 B 地,他们离出发地的距离s和行驶时间t之间的关系的图象如图,根据图象回答下列问题:
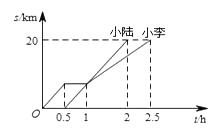
(1)小李在途中逗留的时间为h,小陆从 A 地到 B 地的速度是km/h.
(2)当小李和小陆相遇时,他们离 B 地的路程是千米;
(3)写出小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=
 AB.
AB.(1)求证:EF⊥AG;
(2)若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当
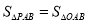 ,求△PAB周长的最小值.
,求△PAB周长的最小值.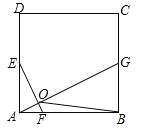
-
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=x2﹣12x化为形如y=a(x﹣h)2+k的形式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知正多边形的每个外角都是45°,则从这个正多边形的一个顶点出发,共可以作_______条对角线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知面包店的面包一个15元,小明去此店买面包,结账时店员告诉小明:“如果你再多买一个面包就可以打九折,价钱会比现在便宜45元”,小明说:“我买这些就好了,谢谢.”根据两人的对话,判断结账时小明买了多少个面包?( )
A.39
B.40
C.41
D.42 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;(3)全等三角形的周长相等;(4)周长相等的两个三角形相等;(5)全等三角形的面积相等;(6)面积相等的两个三角形全等.其中不正确的是( )
A. (4)(5) B. (4)(6) C. (3)(6) D. (3)(4)(5)(6)
相关试题

