【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题:
探究:(1)若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是 ;如图2,当a= °时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:(3)如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;
cosα= (用含有R、m的代数式表示)
拓展:(4)如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 ,并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)

参考答案:
【答案】(1)![]() +1;60°;(2)4+2
+1;60°;(2)4+2![]() ;(3)
;(3)![]() ;(4)
;(4)![]() m2.
m2.
【解析】试题分析:(1)如图1中,作O′E⊥AB于E,MF⊥O′E于F.则四边形AMFE是矩形,EF=AM=1.如图2中,设切点为F,连接O′F,作O′E⊥OA于E,则四边形O′EAF是矩形,在Rt△O′EM中,由sinα=![]() ,推出α=60°.
,推出α=60°.
(2)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.列出方程即可解决问题.
(3)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.列出方程即可解决问题、
(4)当半圆与射线AB相切时,之后开始出现两个交点,此时α=90°;当N′落在AB上时,为半圆与AB有两个交点的最后时刻,此时∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,当半圆弧线与射线AB有两个交点时,α的取值范围是:90°<α≤120°.当N′落在AB上时,阴影部分面积最大,求出此时的面积即可.
试题解析:(1)如图1中,作O′E⊥AB于E,MF⊥O′E于F.则四边形AMFE是矩形,EF=AM=1.想办法求出O′E的长即可.
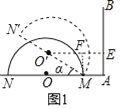
在Rt△MFO′中,∵∠MO![]() F=30°,MO′=2,
F=30°,MO′=2,
∴O′F=O′Mcos30°=![]() ,O′E=
,O′E=![]() +1,
+1,
∴点O′到AB的距离为![]() +1.
+1.
如图2中,设切点为F,连接O′F,作O′E⊥OA于E,则四边形O′EAF是矩形,

∴AE=O′F=2,
∵AM=1,
∴EM=1,
在Rt△O′EM中,sinα=![]() ,
,
∴α=60°
故答案为![]() +1,60°.
+1,60°.
(2)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.
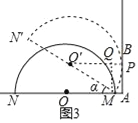
∵O′P=R,
∴R=![]() R+1,
R+1,
∴R=4+2![]() .
.
(3)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.
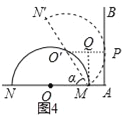
在Rt△O′QM中,O′Q=Rcosα,QP=m,
∵O′P=R,
∴Rcosα+m=R,
∴cosα=![]() .
.
故答案为![]() .
.
(4)如图5中,
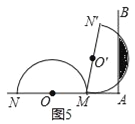
当半圆与射线AB相切时,之后开始出现两个交点,此时α=90°;当N′落在AB上时,为半圆与AB有两个交点的最后时刻,此时∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,当半圆弧线与射线AB有两个交点时,α的取值范围是:90°<α≤120°
故答案为90°<α≤120°;
当N′落在AB上时,阴影部分面积最大,
所以S═![]() ﹣
﹣![]()
![]() m
m![]() m=
m=![]() m2.
m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=
 ,反比例函数y=
,反比例函数y= 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
A. 60 B. 80 C. 30 D. 40
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.


(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】自国家实行一系列“三农”优惠政策后,农民收入大幅度增加,某乡镇所辖村庄去年的年人均收入(单位:元)情况如表:
年人均收入
10500
10700
10800
10900
11500
村庄个数
1
1
3
3
1
该乡去年各村庄年人均收入的中位数是( )
A. 10700 B. 10800 C. 10850 D. 10900
-
科目: 来源: 题型:
查看答案和解析>>【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元)
2
种植树木利润y1(万元)
4
种植花卉利润y2(万元)
2
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣2x+1向上平移2个单位后,所得抛物线的顶点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:
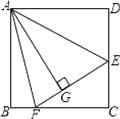
(1)△ABF与△ AGF全等吗?说明理由;
(2)求∠EAF的度数;
(3)若AG=4,△AEF的面积是6,求△CEF的面积.
相关试题

