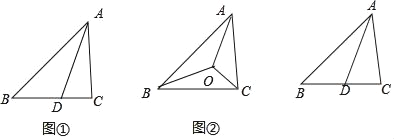
【题目】(发现)(1)如图1,在△ABC中,AD是∠BAC的平分线,对于以下结论:
①AD是△ABC的中线;②S△ABD:S△ACD=AB:AC;③AB:AC=BD:DC,
其中正确的是 (只填序号)
(探究)(2)请你选择(1)中正确的一个选项,简述理由
(应用)(3)如图2,△ABC的三个内角的角平分线相交于点O,且AB=40,BC=48,AC=32,则SABO:S△BCO:S△ACO= : :
(拓展)(4)在(1)中的条件下,过点D作DE⊥AB于点E,DF⊥AB于点F,连接EF,求证:AD垂直平分EF.
参考答案:
【答案】(1)②③;(2)见解析;(3)5,6,4;(4)证明见解析.
【解析】
(1)根据角平分线的性质和三角形面积公式逐一判断可得;
(2)②由AD平分∠BAC知点D到AB、AC的距离相等,设为h,由S△ABD=![]() ABh,S△ACD=
ABh,S△ACD=![]() ACh可判断结论②;③作AP⊥BC,由S△ABD=
ACh可判断结论②;③作AP⊥BC,由S△ABD=![]() BDAP,S△ACD=
BDAP,S△ACD=![]() CDAP知S△ABD:S△ACD=BD:CD,结合S△ABD:S△ACD=AB:AC可得答案;
CDAP知S△ABD:S△ACD=BD:CD,结合S△ABD:S△ACD=AB:AC可得答案;
(3)作OE⊥AB于E,OF⊥BC于F,OG⊥AC于G,根据角平分线的性质知OE=OF=OG,根据S△ABO=![]() ABOE,S△BCO=
ABOE,S△BCO=![]() BCOF,S△ACO=
BCOF,S△ACO=![]() ACOG可得答案;
ACOG可得答案;
(4)根据角平分线上的点到角的两边的距离相等可得DE=DF,再利用“HL”证明△ADE和△ADF全等,根据全等三角形的可得AE=AF,再利用等腰三角形的证明即可.
(1)正确的是②③,
故答案为:②③.
(2)②∵AD平分∠BAC,
∴点D到AB、AC的距离相等,设为h,
则S△ABD=![]() ABh,S△ACD=
ABh,S△ACD=![]() ACh,
ACh,
∴S△ABD:S△ACD=AB:AC;
③如图1,作AP⊥BC于点P,

则S△ABD=![]() BDAP,S△ACD=
BDAP,S△ACD=![]() CDAP,
CDAP,
∴S△ABD:S△ACD=BD:CD,
又∵S△ABD:S△ACD=AB:AC,
∴AB:AC=BD:CD.
(3)如图2,过点O作OE⊥AB于E,OF⊥BC于F,OG⊥AC于G,
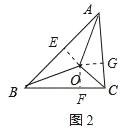
∵AO,BO,CO分别平分∠BAC,∠ABC,∠ACB,
∴OE=OF=OG,
∵S△ABO=![]() ABOE,S△BCO=
ABOE,S△BCO=![]() BCOF,S△ACO=
BCOF,S△ACO=![]() ACOG,
ACOG,
∴SABO:S△BCO:S△ACO=AB:BC:AC=40:48:32=5:6:4,
故答案为:5:6:4;
(4)如图3,

∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在△ADE和△ADF中,
∵![]() ,
,
∴△ADE≌△ADF(HL),
∴AE=AF,
又∵AD平分∠BAC,
∴AD垂直平分EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。

证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:
 (即AB:BC=1:
(即AB:BC=1:  ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)下面是李老师带领同学们探索
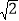 的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是
的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是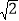 ,且
,且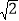 >1,则设
>1,则设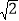 =1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即
=1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即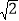 =1+x≈ .
=1+x≈ .(2)请仿照(1)中的方法,若设
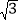 =1.7+y(0<y<1),求
=1.7+y(0<y<1),求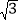 的近似值(要求画出示意图,标明数据,并将
的近似值(要求画出示意图,标明数据,并将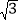 的近似值精确到千分位)
的近似值精确到千分位)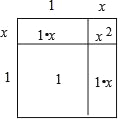
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,D在BC的延长线上,∠ABC与∠ACD的平分线相交于点P,则下列结论中不一定正确的是( )
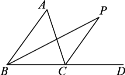
A. ∠ACD=2∠A B. ∠A=2∠P C. BP⊥AC D. BC=CP
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角” (如图)就是一例.这个三角形给出了
 (n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着
展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着 展开式中各项的系数,等等.
展开式中各项的系数,等等.
有如下三个结论:
①当a=1,b=1时,代数式
 的值是1;
的值是1;②当a=-1,b=2时,代数式
 的值是1;
的值是1;③当代数式
 的值是1时,a的值是-2或-4.
的值是1时,a的值是-2或-4.上述结论中,所有正确结论的序号为( )
A. ①② B. ② C. ③ D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(6x4﹣4x3+2x2)÷(﹣2x2)+3x2
(2)(x﹣5)(2x+5)+2x(3﹣x)
(3)(﹣1)2016+(﹣
 )﹣2﹣(3.14﹣π)0
)﹣2﹣(3.14﹣π)0(4)运用乘法公式计算:1122﹣113×111
相关试题

