【题目】如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(8,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
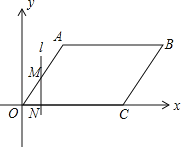
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤12),求S与t的函数表达式;
(3)在(2)的条件下,t为何值时,S最大?并求出S的最大值.
参考答案:
【答案】(1)A(4,4![]() ),B(12,4
),B(12,4![]() );(2)①0≤t≤4时,S=
);(2)①0≤t≤4时,S=![]() t2;②当4<t≤8时,S=2
t2;②当4<t≤8时,S=2![]() t;③当8<t≤12时,S=﹣
t;③当8<t≤12时,S=﹣![]() t2+6
t2+6![]() t;(3)当t=8时,S最大=16
t;(3)当t=8时,S最大=16![]()
【解析】
(1)过点A作AD⊥OC于D,根据菱形的性质可得OA=AB=BC=CO=8,然后根据锐角三角函数即可求出OD和AD,从而求出点A和点B的坐标;
(2)根据直线l与菱形相交的情况分类讨论,分别画出对应的图形,然后根据锐角三角函数和三角形的面积公式计算即可;
(3)利用一次函数增减性和二次函数的增减性分别求出(2)中S的最值,最后取S的最大值即可.
解:(1)过点A作AD⊥OC于D,
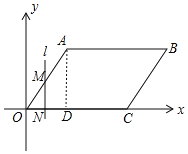
∵四边形OABC为菱形,点C的坐标为(8,0),
∴OA=AB=BC=CO=8.
∵∠AOC=60°,
∴OD=OA·cos∠AOD=4,AD=OA·sin∠AOD=4![]() .
.
∴A(4,4![]() ),B(12,4
),B(12,4![]() );
);
(2)直线l从y轴出发,沿x轴正方向运动与菱形OABC的两边相交有三种情况:
①0≤t≤4时,直线l与OA、OC两边相交,(如图①).
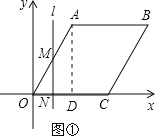
∵MN⊥OC,
∴ON=t.
∴MN=ONtan60°=![]() t.
t.
∴S=![]() ONMN=
ONMN=![]() t2;
t2;
②当4<t≤8时,直线l与AB、OC两边相交,(如图②).
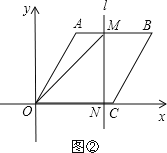
S=![]() ONMN=
ONMN=![]() ×t×4
×t×4![]() =2
=2![]() t;
t;
③当8<t≤12时,直线l与AB、BC两边相交,(如图③).

设直线l与x轴交于点H.
∵MN=4![]() ﹣
﹣![]() (t﹣8)=12
(t﹣8)=12![]() ﹣
﹣![]() t,
t,
∴S=![]() OHMN=
OHMN=![]() ×t×(12
×t×(12![]() ﹣
﹣![]() t)
t)
=﹣![]() t2+6
t2+6![]() t;
t;
(3)由(2)知,当0≤t≤4时,S=![]() t2中,
t2中,![]() >0,对称轴为直线t=0
>0,对称轴为直线t=0
∴当t>0时,S随t的增大而增大
∴S最大=![]() ×42=8
×42=8![]() ,
,
当4<t≤8时,S=2![]() t中,2
t中,2![]() >0
>0
∴S随t的增大而增大
∴S最大=2![]() ×8=16
×8=16![]() ,
,
当8<t≤12时,S=﹣![]() t2+6
t2+6![]() t=﹣
t=﹣![]() (t﹣6)2+18
(t﹣6)2+18![]() 中,﹣
中,﹣![]() <0,对称轴为直线t=6
<0,对称轴为直线t=6
∴当t>6时,S随t的增大而减小
∴当8<t≤12时,S<16![]()
综上所述,当t=8时,S最大=16![]() .
.
-
科目: 来源: 题型:
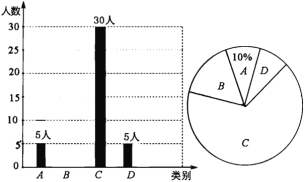
查看答案和解析>>【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季试销售成本为每千克18元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元.经试销发现,销售量y(kg)与销售单价x(元/kg)符合一次函数关系,如图是y与x的函数关系图象.
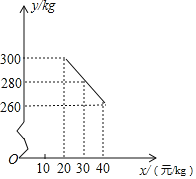
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.

-
科目: 来源: 题型:
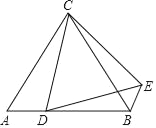
查看答案和解析>>【题目】如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D,若BC=6,sin∠BAC=
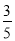 ,则AC=_____,CD=_____.
,则AC=_____,CD=_____.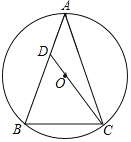
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=2
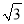 ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.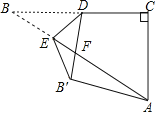
相关试题

