【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在 ![]() 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 .
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 . 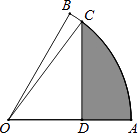
参考答案:
【答案】2π﹣4
【解析】解:∵OC=4,点C在 ![]() 上,CD⊥OA, ∴DC=
上,CD⊥OA, ∴DC= ![]() =
= ![]()
∴S△OCD= ![]() OD
OD ![]()
∴ ![]() =
= ![]() OD2(16﹣OD2)=﹣
OD2(16﹣OD2)=﹣ ![]() OD4+4OD2=﹣
OD4+4OD2=﹣ ![]() (OD2﹣8)2+16
(OD2﹣8)2+16
∴当OD2=8,即OD=2 ![]() 时△OCD的面积最大,
时△OCD的面积最大,
∴DC= ![]() =
= ![]() =2
=2 ![]() ,
,
∴∠COA=45°,
∴阴影部分的面积=扇形AOC的面积﹣△OCD的面积= ![]() ﹣
﹣ ![]() ×2
×2 ![]() ×2
×2 ![]() =2π﹣4,
=2π﹣4,
所以答案是:2π﹣4.
【考点精析】解答此题的关键在于理解二次函数的最值的相关知识,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )

A.1:3
B.1:5
C.1:6
D.1:11 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形硬纸片ABCD中,
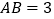 ,
,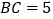 ,
, ,沿着对角线BD将平行四边形剪开成两个三角形,固定
,沿着对角线BD将平行四边形剪开成两个三角形,固定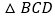 不动,将
不动,将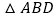 沿射线BD方向以每秒1个单位的速度匀速运动
沿射线BD方向以每秒1个单位的速度匀速运动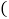 运动后
运动后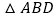 记为
记为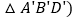 连接
连接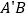 和
和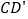 .
.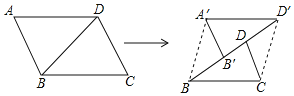
 小明认为在运动过程中,始终有
小明认为在运动过程中,始终有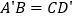 ,你同意吗?请说明理由.
,你同意吗?请说明理由.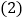 保持上述条件不变,当
保持上述条件不变,当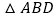 运动______秒时,四边形
运动______秒时,四边形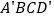 为菱形.
为菱形. 保持上述条件不变,当
保持上述条件不变,当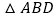 运动______秒时,四边形
运动______秒时,四边形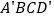 为矩形.
为矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正比例函数
 与反比例函数
与反比例函数 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为 其中
其中 .
. 四边形ABCD的是______
四边形ABCD的是______ 填写四边形ABCD的形状
填写四边形ABCD的形状
 当点A的坐标为
当点A的坐标为 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值. 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】采摘茶叶是茶农一项很繁重的劳动,利用单人便携式采茶机能大大提高生产效率.实践证明,一台采茶机每天可采茶60公斤,是人手工采摘的5倍,购买一台采茶机需2400元.茶园雇人采摘茶叶,按每采摘1公斤茶叶m元的标准支付雇工工资,一个雇工手工采摘茶叶20天获得的全部工钱正好购买一台采茶机.
(1)求m的值;
(2)有两家茶叶种植户王家和顾家均雇人采摘茶叶,王家雇用的人数是顾家的2倍.王家所雇的人中有
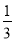 的人自带采茶机采摘,
的人自带采茶机采摘, 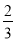 的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶? -
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用问题:
一个蓄水池装有甲、乙两个进水管和丙一个出水管,单独开放甲管3小时可注满一池水,单独开放乙管6小时可注满一池水,单独开放丙管4小时可放尽一池水.
(1)若同时开放甲、乙、丙三个水管,几小时可注满水池?
(2)若甲管先开放1小时,而后同时开放乙、丙两个水管,则共需几小时可注满水池?
(3)若甲管先开放1小时后关闭,而后同时开放乙、丙两个水管,能注满水池吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
相关试题

