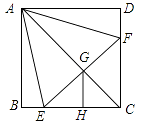
【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若 ![]() ,则
,则 ![]() =( )
=( )
A.6
B.4
C.3
D.2
参考答案:
【答案】A
【解析】∵四边形ABCD是正方形,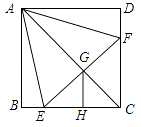
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°,
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
∵AE=AF,AB=AD,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∴△CEF是等腰直角三角形,
∵AE=AF,
∴AC垂直平分EF,
∴EG=GF,
∵GH⊥CE,
∴GH∥CF,
∴△EGH∽△EFC,
∵S△EGH=3,
∴S△EFC=12,
∴CF= ![]() ,EF=
,EF= ![]() ,
,
∴AF= ![]() ,设AD=x,则DF=x﹣
,设AD=x,则DF=x﹣ ![]() ,
,
∵AF2=AD2+DF2 ,
∴( ![]() )2=x2+(x﹣
)2=x2+(x﹣ ![]() )2 ,
)2 ,
∴x= ![]() ,
,
∴AD= ![]() ,DF=
,DF= ![]() ,
,
∴S△ADF= ![]() ADDF=6.
ADDF=6.
故答案为:A.
根据正方形的性质及等边三角形的性质易证明AE=AF,AB=AD,根据直角三角形全等判定证明Rt△ABE≌Rt△ADF,得出BE=DF,从而证得CE=CF,得出△CEF是等腰直角三角形,再证明GH∥CF,得出△EGH∽△EFC,根据相似三角形的性质及S△EGH=3,求出△EFC的面积,从而求出AF和CE的长,然后设AD=x,利用勾股定理求出AD的长及DF的长,根据三角形的面积公式即可得出答案。
-
科目: 来源: 题型:
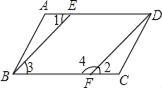
查看答案和解析>>【题目】如图,已知AD∥BC,∠3+∠4=180°,要证∠1=∠2,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知)
∴∠l=∠3( ),
∵∠3+∠4=180°(已知),
∴BE∥DF( ),
∴ = ( ).
∴∠1=∠2( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=-x+1(0≤x≤10)与反比例函数y=
 (-10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(-10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
A.- ≤x≤1
≤x≤1
B.- ≤x≤
≤x≤ 
C.- ≤x≤
≤x≤ 
D.1≤x≤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在
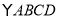 中,点
中,点 、
、 分别是
分别是 、
、 边的中点,
边的中点,  、
、 是对角线
是对角线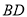 上的两点,且
上的两点,且 ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.
 B.
B. 
C.
 ∥
∥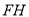 D. 四边形
D. 四边形 是平行四边形
是平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
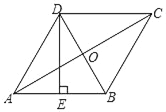
A. 18 B. 18
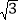 C. 9
C. 9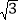 D. 6
D. 6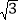
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是反比例函数
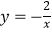 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 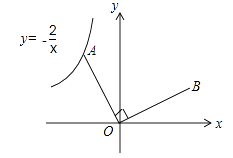
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“汉字听写”大赛中,准备一次性购买若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为优胜者的奖品,已知购买3支钢笔和4本笔记本共需88元,购买4支钢笔和5本笔记本共需114元.
(1)求购买一支钢笔和一本笔记本各需多少元?
(2)学校准备购买钢笔和笔记本共80件奖品,根据规定购买的总费用不能超过1200元,求最多可以购买多少支钢笔?
相关试题

