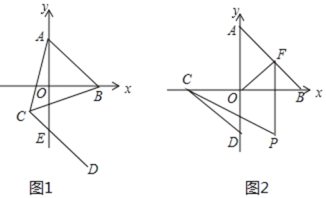
【题目】.如图 1,在平面直角坐标系中,A 、B 在坐标轴上,其中 A(0, a) ,B(b, 0)满足| a 3 |![]() 0.
0.
(1)求 A 、 B 两点的坐标;
(2)将 AB 平移到CD , A 点对应点C(2, m) , DE 交 y 轴于 E ,若ABC 的面积等于13,求点 E 的坐标;
(3)如图 2,若将 AB 平移到CD ,点 C、D 也在坐标轴上,F 为线段 AB 上一动点,(不包括点 A ,点B) ,连接OF 、FP 平分BFO ,BCP 2PCD,试探究COF,OFP ,CPF 的数量关系.
参考答案:
【答案】(1)A(0,3),B(4,0);(2)E的坐标为(0,![]() );(3)∠COF+∠OFP=3∠CPF.
);(3)∠COF+∠OFP=3∠CPF.
【解析】
(1)根据非负数的性质分别求出a、b,得到答案;
(2)构造矩形,根据三角形的面积是13,利用割补法求出m,再根据平移的性质,求出直线DC的解析式,则可求出点E的坐标;
(3)作HP∥AB交AD于H,OG∥AB交FP于G,设∠OFP=x,∠PCD=y,根据平行线的性质、三角形的外角的性质计算即可.
解:(1)由题意得,a-3=0,b-4=0,
解得,a=3,b=4,
则A(0,3),B(4,0);
(2)如图1所示,

∵ABC的面积等于13,根据A,B,C三点的坐标,
可得:![]() ,(m<0)
,(m<0)
解得,m=-2,
则点C的坐标为(-2,-2),
根据平移规律,则有点D的坐标为(2,-5),
设直线CD的解析式为:y=cx+d,
![]() ,解得
,解得 ,
,
∴CD的解析式为:![]() ,
,
∴CD与y轴的交点E的坐标为(0,![]() );
);
(3)如图2所示,作HP∥AB交AD于H,OG∥AB交FP于G,

设∠OFP=x,∠PCD=y,
则∠BFP=x,∠PCB=2y,
∵HP∥AB,OG∥AB,
∴∠HPC=∠PCD=y,∠OPF=∠OFP=x,
∴∠CPF=x+y,
又∵∠COF=∠PCB +∠CPF +∠OFP =2y+(x+y)+ x =2x+3y,
∴∠COF+∠OFP=3x+3y=3∠CPF.
-
科目: 来源: 题型:
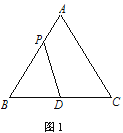
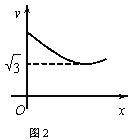
查看答案和解析>>【题目】如图1,在等边△ABC中,D是BC的中点,P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则△ABC的面积为( )
A. 4 B.
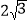 C. 12 D.
C. 12 D. 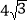
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为
 ,则a的值是( )
,则a的值是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
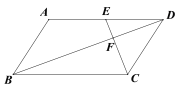
查看答案和解析>>【题目】如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF =3,则S□ABCD =_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列四个结论:①AP=EF;②△APD一定是等腰三角形;③∠PFE=∠BAP;④PD=
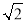 EC,其中正确结论的序号是_______.
EC,其中正确结论的序号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司10名销售员,去年完成的销售额情况如表:
销售额(单位:万元)
3
4
5
6
7
8
10
销售员人数(单位:人)
1
3
2
1
1
1
1
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
相关试题

